Ravon R2: размеры и подробное техописание — акпп, двигатель, клиренс
| Название | R2 |
|---|---|
| Кузов | |
| Количество посадочных мест | 5 |
| Тип | Хетчбек |
| Размеры | |
| Высота, мм | 1522 мм |
| Длина, мм | 3640 мм |
| Колесная база, мм | 2375 мм |
| Ширина, мм | 1597 мм |
| Двигатель | |
| Аккумулятор 12V, А/ч | 50AH |
| Генератор, A | 100A |
| Диаметр и ход поршня, мм | 70,5/80 |
| Количество клапанов | 16 |
Макс. крутящий момент, Нм/об. мин крутящий момент, Нм/об. мин | 112.5 / 4200 |
| Максимальная мощность, кВт | 62.6 кВт/ 85.1л.с. /6400об.мин |
| Материал блока цилиндров и головки | чугун / алюминий |
| Моторное масло, л. | 4,0 |
| Охлаждающая жидкость, л. | 4,74 |
| Рабочий объем, см.куб | 1249 см³ |
| Расположение двигателя | спереди, поперечный |
| Расположение клапанов | 4 клапана на цилиндр |
| Система зажигания | Прямое зажигание без распределителя |
| Система охлаждения | жидкостная, закрытая система |
| Система питания | Многоточечный впрыск топлива |
| Степень сжатия | 10,5 |
| Тип | В ряд; 4-цилиндровый |
| Тип и марка топлива | Неэтилированный |
| Топливный насос | Электрический насос |
| Число и расположение цилиндров | 4 |
| Трансмиссия | |
| Передаточное число (1/2/3/4/задняя/главная) | 2,875 / 1,568 / 1,000 / 0,697 / 2,300 / 4,145 |
| Тип привода | Передний |
| Тип сцепления | Автоматический |
| Тип трансмиссии | Автоматический |
| Объемы и массы | |
Макс. нагрузка осей пер./зад., кг, кг нагрузка осей пер./зад., кг, кг | 750 / 700 |
| Объем багажника, л | 170(VDA) |
| Объем топливного бака, л | 35 |
| Полная масса / макс. допустимая масса, кг, кг. | 950~1,363 |
| Снаряженная масса автомобиля, кг, кг. | 1054 |
| Динамические характеристики | |
| Максимальная скорость, км/ч, км/ч | 161 |
| Разгон до 100 км/ч с места, cекунд, с | 12,4 |
| Тормозная система | |
| ABS | 4х сенсорный |
| Задние тормоза | Барабанные, Φ200 |
| Передние тормоза | Дисковые, Φ237 |
| Подвеска | |
| Задняя подвеска | Полузависимая, торсионная |
| Передняя подвеска | Тип Макферсон |
| Размер диска | 4,5Jx13 / 4,5Jx14 |
| Рулевое управление | Электрический |
| Шины | 155/80 R13 / 155/70 R14 |
| Расход топлива (литр/100км) | |
| Городской цикл, л | 8,2 |
| Загородный цикл, л | 5,1 |
| Смешанный цикл, л | 6,2 |
| Эксплуатационные показатели | |
| Выбросы CO2, г/км, г/км | 145 |
| Экологический класс | Euro 5 |
Технические характеристики Равон Р2 (Ravon R2) 2019 годов выпуска
Модификации по годам
2019201820172016
| Модификация | Тип кузова | Объём | Мощность | Года выпуска |
Ravon R2 Comfort 1. 2 AT автомат бензин
хэтчбек, 1249 см3, 85 л.с., 2016 — 2019 г.в 2 AT автомат бензин
хэтчбек, 1249 см3, 85 л.с., 2016 — 2019 г.в | хэтчбек | 1249 см3 | 85 л.с. | 2016 — 2019 |
| Ravon R2 Elegant 1.2 AT автомат бензин хэтчбек, 1249 см3, 85 л.с., 2016 — 2019 г.в | хэтчбек | 1249 см3 | 85 л.с. | 2016 — 2019 |
| Ravon R2 Optimum 1.2 AT автомат бензин хэтчбек, 1249 см3, 85 л.с., 2016 — 2019 г.в | хэтчбек | 1249 см3 | 85 л.с. | 2016 — 2019 |
Модификации других годов: 2018, 2017, 2016
Выберите поколение R2
Продажа Ravon R2
| Ravon R2 | 2018 | 48 606 км | 645 000 Р | |
1.20 л, бензин хэтчбек, серебряный автомат 13″ стальные колесные диски Москва, 5 часов назад 3 Показать телефон Сравнить | ||||
| Ravon R2 | 2016 | 52 000 км | 620 000 Р | |
1.20 л, бензин хэтчбек, красный автомат Москва, 3.09.2022 1 Показать телефон Сравнить | ||||
| Ravon R2 | 2018 | 67 725 км | 670 000 Р | |
1.20 л, бензин хэтчбек, белый автомат Москва, 1.09.2022 0 Показать телефон Сравнить | ||||
| Ravon R2 | 2018 | 48 606 км | 705 000 Р | |
1. Москва, 4.08.2022 0 Показать телефон Сравнить | ||||
| Ravon R2 | 2016 | 75 000 км | 683 000 Р | |
1.20 л(85 л.с.), бензин хэтчбек, серый автомат, Comfort 1.2 AT Москва, 2.09.2022 0 Показать телефон Сравнить | ||||
| Ravon R2 | 2016 | 73 000 км | 770 000 Р | |
1.20 л(85 л.с.), бензин хэтчбек, серебряный автомат, Comfort 1.2 AT Москва, 28.08.2022 0 Показать телефон Сравнить | ||||
| Ravon R2 | 2017 | 41 000 км | 499 000 Р | |
1. Москва, вчера 0 Показать телефон Сравнить | ||||
| Ravon R2 | 2017 | 18 096 км | 850 000 Р | |
1.30 л, бензин хэтчбек, красный автомат, Comfort 1.2 AT Москва, 7.09.2022 1 Показать телефон Сравнить | ||||
| Ravon R2 | 2019 | 50 км | 767 500 Р | |
1.20 л, бензин хэтчбек, серый автомат Москва, 12.03.2022 58 Показать телефон Сравнить | ||||
| Ravon R2 | 2019 | 50 км | 1 051 000 Р | |
1. Москва, 27 декабря 21 г. 1 Показать телефон Сравнить | ||||
Все объявления о продаже Ravon R2
Отзывы о Ravon R2
Ravon R2 2017
9.1 (9.1/10)
Один из самых дешевых автомобилей с АКПП, купили его жене, она очень довольна, ездит на нем уже три месяца, все работает исправно.
4 апреля 2018 г.
Ravon R2 2017
9.1 (9.1/10)
Один из самых дешевых автомобилей с АКПП, купили его жене, она очень довольна, ездит на нем уже три месяца, все работает исправно.
4 апреля 2018 г.
Смотреть все
Форум и вопросы-ответы
Все темы
Посмотреть все
Материалы о Ravon
Все комплектации и технические характеристики автомобилей Ravon R2, как официально поставляемых в РФ, так и ттх остальных авто. Тут можно узнать подробное техническое
описание Равон Р2 от первых до современных моделей, узнать про расход топлива и габариты, кузове и двигателях, коробке передач и тормозной системе.
Рейтинги машин
Технические характеристики Равон Р2
| Характеристика | 1.3 AT 85 л.с. бензин передний |
|---|---|
| Краткая информация | |
| Объем | 1.3 |
| Мощность | 85 |
| Коробка | автомат |
| Топливо | бензин |
| Запас хода | 0 |
| Разгон | 0 |
| Расход | 0 |
| Общая информация | |
| Страна марки | |
| Класс автомобиля | A |
| Количество дверей | 5 |
| Количество мест | 5 |
| Безопасность | |
| Оценка безопасности | |
| Название рейтинга | |
| Размеры, мм | |
| Длина | 3640 |
| Ширина | 1597 |
| Высота | 1522 |
| Колёсная база | 2375 |
| Клиренс | 160 |
| Ширина передней колеи | 0 |
| Ширина задней колеи | 0 |
| Размер колёс | 155/70/R14 |
| Объём и масса | |
| Объем багажника мин/макс, л | 170 |
| Объём топливного бака, л | 35 |
| Снаряженная масса, кг | 950 |
| Полная масса, кг | 1363 |
| Трансмиссия | |
| Коробка передач | автомат |
| Количество передач | 4 |
| Тип привода | передний |
| Подвеска и тормоза | |
| Тип передней подвески | независимая, пружинная |
| Тип задней подвески | полунезависимая, пружинная |
| Передние тормоза | дисковые |
| Задние тормоза | барабанные |
| Эксплуатационные показатели | |
| Максимальная скорость, км/ч | 161 |
| Разгон до 100 км/ч, с | 12. 4 4 |
| Марка топлива | АИ-95 |
| Экологический класс | |
| Выбросы CO2, г/км | 0 |
| Расход топлива, л город/трасса/смешанный | |
| Расход топлива, л смешанный | |
| Расход топлива, л город/смешанный | |
| Расход топлива, л город/трасса | |
| Расход топлива, л город | |
| Расход топлива, л трасса | |
| Расход топлива, л трасса/смешанный | |
| Двигатель | |
| Тип двигателя | бензин |
| Расположение двигателя | переднее, поперечное |
| Объем двигателя, см³ | 1249 |
| Тип наддува | нет |
Максимальная мощность, л. с./кВт при об/мин с./кВт при об/мин | 85 / 63 при 6400 |
| Максимальный крутящий момент, Н*м при об/мин | |
| Расположение цилиндров | рядное |
| Количество цилиндров | 4 |
| Число клапанов на цилиндр | 4 |
| Система питания двигателя | распределенный впрыск (многоточечный) |
| Степень сжатия | 10. 5 5 |
| Диаметр цилиндра и ход поршня, мм | 70.5 × 80 |
| Аккумуляторная батарея | |
| Запас хода на электричестве, км | 0 |
| Емкость батареи, кВт⋅ч | 0 |
| Время зарядки, ч | 0 |
Технические характеристики Равон Р2 – Авис Авто
Технические характеристики Равон Р2 – Авис Авто- Brilliance
- Changan
- Chery
- Cheryexeed
- Chevrolet
- Citroen
- Datsun
- Dongfeng
- Faw
- Foton
- Gac
- Geely
- Great Wall
- Haval
- Hawtai
- Hyundai
- Jac
- Kia
- Lada
- Lifan
- Mazda
- Mitsubishi
- Nissan
- Opel
- Peugeot
- Ravon
- Renault
- Skoda
- Ssangyong
- Suzuki
- Toyota
- Uaz
- Volkswagen
- Zotye
г. Москва, Краснобогатырская, 89с4
Москва, Краснобогатырская, 89с4
8 800 500-83-42 Заказать звонок
R2
ПОЛУЧИТЬ СПЕЦИАЛЬНОЕ ПРЕДЛОЖЕНИЕ
В кредит от 6 400 р/мес.
Нажимая на кнопку, вы даете согласие на обработку своих персональных данныхR2
ПОЛУЧИТЬ СПЕЦИАЛЬНОЕ ПРЕДЛОЖЕНИЕ
В кредит от 6 400 р/мес.
Нажимая на кнопку, вы даете согласие на обработку своих персональных данныхЧасто задаваемые вопросы про Ravon R2
Какой клиренс у Ravon R2?
Дорожный просвет у автомобиля Ravon R2 составляет 160 мм.

Фары у Ravon R2 – какие они?
В базовой версии фары Галогенные.
Какой двигатель у Ravon R2?
Ravon R2 оснащается следующими типами двигателей —
- 1.3 мощностью 85 л.с. (бензин)
org/Question»>Каков минимальный объем багажника у Ravon R2?
Объем багажного отделения у автомобиля Ravon R2, составляет 170 литров.
Сколько Ravon R2 расходует бензина в условиях города?
Средний расход Ravon R2 составляет 8.
 9 литров на 100 км.
9 литров на 100 км.
Каков разгон Ravon R2 до 100км/ч?
Разгон у автомобиля Ravon R2, по ТХ с завода составляет 12.4 секунд.
Краткая информация
| 1.3 AT | |
|---|---|
| Объем | 1.3 |
| Мощность | 85 |
| Коробка | автомат |
| Топливо | бензин |
Общая информация
| 1.3 AT | |
|---|---|
| Класс автомобиля | A |
| Количество дверей | 5 |
| Количество мест | 5 |
| Страна марки | Узбекистан |
Размеры, мм
| 1.3 AT | |
|---|---|
| Длина | 3640 |
| Ширина | 1597 |
| Высота | 1522 |
| Колёсная база | 2375 |
| Клиренс | 160 |
| Размер колёс | 155/70/R14 |
Объём и масса
1. 3 AT 3 AT | |
|---|---|
| Объем багажника мин/макс, л | 170 |
| Объём топливного бака, л | 35 |
| Снаряженная масса, кг | 950 |
| Полная масса, кг | 1363 |
Трансмиссия
| 1.3 AT | |
|---|---|
| Коробка передач | автомат |
| Количество передач | 4 |
| Тип привода | передний |
Подвеска и тормоза
| 1.3 AT | |
|---|---|
| Тип передней подвески | независимая, пружинная |
| Тип задней подвески | полунезависимая, пружинная |
| Передние тормоза | дисковые |
| Задние тормоза | барабанные |
Эксплуатационные показатели
| 1.3 AT | |
|---|---|
| Максимальная скорость, км/ч | 161 |
| Разгон до 100 км/ч, с | 12. 4 4 |
| Марка топлива | АИ-95 |
| Расход топлива, л город/трасса/смешанный | 8.2/5.1/6.2 |
Двигатель
| 1.3 AT | |
|---|---|
| Тип двигателя | бензин |
| Расположение двигателя | переднее, поперечное |
| Объем двигателя, см³ | 1249 |
| Тип наддува | нет |
| Максимальная мощность, л.с./кВт при об/мин | 85 / 63 при 6400 |
| Расположение цилиндров | рядное |
| Количество цилиндров | 4 |
| Число клапанов на цилиндр | 4 |
| Система питания двигателя | распределенный впрыск (многоточечный) |
| Степень сжатия | 10.5 |
| Диаметр цилиндра и ход поршня, мм | 70.5 × 80 |
ЗАПИШИТЕСЬ НА ОСМОТР АВТО
Обменяйте свой автомобиль с выгодой до 685 000 р
Конфигуратор Ravon R2
- 1 Модификация
- 2 Комплектация
- 3 Цвет
- 4 Акция
- 5 Подарки
- 6 Ваш авто
Модификация
- 3 AT 85 л.с. бензин передний»> 1.3 AT 85 л.с. бензин передний
Ваш выбор
1.3 AT 85 л.с. бензин передний
| Объем | 1.3 |
| Мощность | 85 |
| Коробка | автомат |
| Топливо | бензин |
| Запас хода | 0 |
| Разгон | 0 |
| Расход | 0 |
| Страна марки | none |
| Класс автомобиля | A |
| Количество дверей | 5 |
| Количество мест | 5 |
| Страна марки | Узбекистан |
| Оценка безопасности | none |
| Название рейтинга | none |
| Длина | 3640 |
| Ширина | 1597 |
| Высота | 1522 |
| Колёсная база | 2375 |
| Клиренс | 160 |
| Ширина передней колеи | 0 |
| Ширина задней колеи | 0 |
| Размер колёс | 155/70/R14 |
| Объем багажника мин/макс, л | 170 |
| Объём топливного бака, л | 35 |
| Снаряженная масса, кг | 950 |
| Полная масса, кг | 1363 |
| Коробка передач | автомат |
| Количество передач | 4 |
| Тип привода | передний |
| Тип передней подвески | независимая, пружинная |
| Тип задней подвески | полунезависимая, пружинная |
| Передние тормоза | дисковые |
| Задние тормоза | барабанные |
| Максимальная скорость, км/ч | 161 |
| Разгон до 100 км/ч, с | 12. 4 4 |
| Марка топлива | АИ-95 |
| Экологический класс | none |
| Выбросы CO2, г/км | 0 |
| Расход топлива, л город/трасса/смешанный | none |
| Расход топлива, л город/трасса/смешанный | 8.2/5.1/6.2 |
| Расход топлива, л смешанный | none |
| Расход топлива, л город/смешанный | none |
| Расход топлива, л город/трасса | none |
| Расход топлива, л город | none |
| Расход топлива, л трасса | none |
| Расход топлива, л трасса/смешанный | none |
| Тип двигателя | бензин |
| Расположение двигателя | переднее, поперечное |
| Объем двигателя, см³ | 1249 |
| Тип наддува | нет |
Максимальная мощность, л. с./кВт при об/мин с./кВт при об/мин | 85 / 63 при 6400 |
| Максимальный крутящий момент, Н*м при об/мин | none |
| Расположение цилиндров | рядное |
| Количество цилиндров | 4 |
| Число клапанов на цилиндр | 4 |
| Система питания двигателя | распределенный впрыск (многоточечный) |
| Степень сжатия | 10.5 |
| Диаметр цилиндра и ход поршня, мм | 70.5 × 80 |
| Запас хода на электричестве, км | 0 |
| Емкость батареи, кВт⋅ч | 0 |
| Время зарядки, ч | 0 |
Ваш выбор
Comfort
Цена: 585 000 р
Безопасность
- Подушка безопасности пассажира
- Антиблокировочная система (ABS)
- Подушка безопасности водителя
- Крепление детского кресла (задний ряд) ISOFIX
Защита от угона
- Центральный замок
- Иммобилайзер
Салон
- Складывающееся заднее сиденье
- Ткань (Материал салона)
Комфорт
- Усилитель руля
- Электростеклоподъёмники передние
Элементы экстерьера
- Стальные диски
- Металлик
Мультимедиа
- USB
- Аудиоподготовка
- AUX
- Аудиосистема
- Розетка 12V
Ваш выбор
Optimum
Цена: 606 000 р
Обзор
- Электрообогрев боковых зеркал
- Электрообогрев зоны стеклоочистителей
Безопасность
- Подушка безопасности пассажира
- Подушки безопасности боковые
- Антиблокировочная система (ABS)
- Подушка безопасности водителя
- Крепление детского кресла (задний ряд) ISOFIX
Защита от угона
- Центральный замок
- Сигнализация
- Иммобилайзер
Салон
- Складывающееся заднее сиденье
- Ткань (Материал салона)
Комфорт
- Электропривод зеркал
- Бортовой компьютер
- Усилитель руля
- Кондиционер
- Электростеклоподъёмники передние
- Регулировка руля по высоте
Элементы экстерьера
- Стальные диски
- Металлик
Мультимедиа
- USB
- Аудиоподготовка
- AUX
- Аудиосистема
- Розетка 12V
Ваш выбор
Elegant
Цена: 627 000 р
Обзор
- Электрообогрев боковых зеркал
- Электрообогрев зоны стеклоочистителей
Безопасность
- Подушка безопасности пассажира
- Подушки безопасности боковые
- Антиблокировочная система (ABS)
- Подушка безопасности водителя
- Крепление детского кресла (задний ряд) ISOFIX
- Подушки безопасности оконные (шторки)
Защита от угона
- Центральный замок
- Сигнализация
- Иммобилайзер
Салон
- Складывающееся заднее сиденье
- Ткань (Материал салона)
- Подогрев передних сидений
Комфорт
- Мультифункциональное рулевое колесо
- Электропривод зеркал
- Бортовой компьютер
- Усилитель руля
- Электростеклоподъёмники задние
- Кондиционер
- Парктроник задний
- Электростеклоподъёмники передние
- Регулировка руля по высоте
Элементы экстерьера
- Рейлинги на крыше
- Диски 14
- Металлик
Мультимедиа
- USB
- Аудиоподготовка
- AUX
- Аудиосистема
- Розетка 12V
ПРЕДЫДУЩИЙ ШАГ СЛЕДУЮЩИЙ ШАГ
Нажимая на кнопку, вы даете согласие на обработку своих персональных данных
Нажимая на кнопку, вы даете согласие на обработку своих персональных данных Нажимая на кнопку, вы даете согласие на обработку своих персональных данныхДвигатель Равон Р2 (Ravon R2): устройство, отзывы, характеристики
Двигатель Равон Р2 — удачной узбекской новинки – это очередная вариация давно всем знакомого базового двигателя, который можно найти и в других машинах Равон, причём как на старых моделях, так и на «рестайлинге». Компоновка и технические характеристики почти не меняются. Это бензиновый «движок» из Chevrolet Spark, специально адаптированный под АКПП. Кстати, купить Р2 можно только с коробкой-автомат.
Компоновка и технические характеристики почти не меняются. Это бензиновый «движок» из Chevrolet Spark, специально адаптированный под АКПП. Кстати, купить Р2 можно только с коробкой-автомат.
Модель и характеристики двигателя Равон Р2
С самого появления модели на рынке, Равон Р2 комплектуют четырёхцилиндровым двигателем внутреннего сгорания, относящимся к серии S-TEC II объёмом 1250 куб. см (фактически 1249). 16-клапанная система газораспределения – одно из заметных достоинств скромного мотора.
ДВС на Равоне Р2 адаптирован под четырёх — или пятиступенчатую АКПП, у авто первый вариант. Мощность двигателя 85 лошадиных сил, это немного, но для малолитражки достаточно. Мотор весьма оборотист, что улучшает потребительские характеристики в эксплуатации.
Два распределительных вала головки дают оптимальное наполнение цилиндро-поршневой группы. Фазы впуска и выпуска при этом изменяемы. Обновлённый блок управления и модернизированная электропроводка позволили мотору получить класс Евро-5.
Двигатель Равон Р2 адаптирован производителем под российские условия эксплуатации. Опыт использования и отзывы автовладельцев говорят о том, что адаптация весьма удачная. Ни сложные климатические условия, ни низкокачественное топливо не выводят мотор из строя.
| Характеристики двигателя Ravon R2 в таблице | |
|---|---|
| Тип | Рядный бензиновый 4-цилиндровый |
| Рабочий объём | 1249 см³ |
| Максимальная мощность | 85 л.с. при 6400 об.мин |
| Максимальный крутящий момент | 112 при 4200 об.мин |
| Количество клапанов | 16 |
| Материал блока цилиндров / головки | чугун / алюминий |
| Привод ГРМ | цепь |
Своевременное ТО обеспечит бесперебойную работу не менее чем на 250 тысяч километров, утверждают на заводе-изготовителе.
Эксплуатация мотора Равон Р2
Одним из главных эксплуатационных преимуществ владельцы узбекской малолитражки называют — экономичность. Он работает на недорогом АИ-92, а расход в городском цикле составит 8,2 л бензина на 100 км, при спокойном стиле езды. За городом и того меньше: 5,1 л на 100 км.
Он работает на недорогом АИ-92, а расход в городском цикле составит 8,2 л бензина на 100 км, при спокойном стиле езды. За городом и того меньше: 5,1 л на 100 км.
Также владельцы отмечают бодрость двигателя, быстрый разгон и беспроблемную службу. Отзывы о моторе владельцев Р2 очень хорошие. Хлопот с ним нет вообще.
Основные достоинства и недостатки ДВС на Ravon R2
Несомненными преимуществами двигателя владельцы Равон считают экономный расход бензина, плавный ход, стандарт Евро-5, редкие поломки и приспособленность к российским условиям эксплуатации. Кроме того, он адаптирован под автоматическую коробку передач, что привлекает к модели всех ценителей удобства и комфорта за приемлемые деньги.
Минусы
Есть однако и минусы, точнее, особенности, с которыми надо считаться. Например, двигатели Равон → весьма требовательны к маслу, которое в них заливают. Некачественный или низкокачественный продукт забьёт масляные каналы, которые сконструированы несколько неудачно – слишком узкие.
Производитель советует использовать масла и фильтры, прошедшие специальную сертификацию, а также покупать запчасти только у официальных дилеров.
В авторизованном сервисном центре специалисты выполняют полную промывку двигателя при замене масла →, что позволяет продлить жизнь ДВС. Чем больше пробег – тем выше риск осложнений от узких масляных каналов.
Индивидуальные черты
У каждой модели авто есть свои особенности по ДВС, которыми делятся автовладельцы на форумах и оставляют отзывы о моторе. Для Равон Р2 одной из основных индивидуальных черт является материал, из которого изготовлен мотор. Это толстостенный чугун. Благодаря такому решению агрегат отлично выдерживает высокие температуры, надёжен и долговечен. Однако, перегревать его всё же не нужно: головка изготовлена из легкоплавкого соединения.
Двигатель оснащён цепью в механизме цилиндро-поршневой группы. Среди автолюбителей принято считать, что моторы на цепном приводе в несколько раз надёжнее, чем на ремнях. Эксплуатация подобных моторов это подтверждает. Если цепь порвётся, клапаны не будут деформированы.
Эксплуатация подобных моторов это подтверждает. Если цепь порвётся, клапаны не будут деформированы.
Ещё одна важная особенность двигателя Ravon R2 – специальные модули коммутации. Они настраивают ДВС на оптимальный режим работы, исходя из температуры окружающей среды и условий поездки. Благодаря этому мотор работает стабильно, независимо от режима использования.
Любителям апгрейдов не составит труда установить в сервисном центре прошивку, которая поднимет производительность ещё на 30%. Также на этот двигатель можно без проблем устанавливать газ.
Двигатель Равон Р2, подстать автомобилю, имеет небольшие размеры. Технические специалисты считают его внешний вид весьма привлекательным. Защита картера установлена во всех комплектациях малолитражки, что очень разумно, учитывая огрехи дорожного покрытия и небольшой клиренс авто.
Подводим итоги
Водители и авто-эксперты сходятся в мнении, что двигатель Равон Р2 – очень удачный и надёжный агрегат, у которого есть большие перспективы по части дальнейших усовершенствований для новых моделей производителя. Узбекский завод не прекращает постоянное усовершенствование своей технологии, увеличивая надёжность и устраняя выявленные недостатки.
Узбекский завод не прекращает постоянное усовершенствование своей технологии, увеличивая надёжность и устраняя выявленные недостатки.
Одно из главных конкурентных преимуществ мотора – его экономичность при неплохих технических характеристиках для авто данного класса. Малый расход, недорогая марка топлива, способность отлично адаптироваться на всех диапазонах оборотов. Есть возможность установить на автомобиль газ (правда придётся пожертвовать багажником). И без того невысокие расходы на ГСМ снизятся в разы.
По обслуживанию ДВС на Равон Р2 – один из самых недорогих. Да, нужно будет потратиться на хорошее масло и сертифицированные запчасти, но масла понадобится всего 3 л, а производство комплектующих отлично налажено в России.
RAVON R2 — Ravon ТЕХНО КАР
| Название | R2 |
|---|---|
| КУЗОВ | |
| Тип | Хетчбек |
| Количество посадочных мест | 5 |
| РАЗМЕРЫ | |
| Длина | 3640 мм |
| Ширина | 1597 мм |
| Высота | 1522 мм |
| Колесная база | 2375 мм |
| ДВИГАТЕЛЬ | |
| Тип | В ряд; 4-цилиндровый |
| Рабочий объем | 1249 см³ |
| Число и расположение цилиндров | 4 |
| Максимальная мощность | 62. 6 кВт/ 85.5 л.с. / 6400 об.мин 6 кВт/ 85.5 л.с. / 6400 об.мин |
| Система питания | Многоточечный впрыск топлива |
| Тип и марка топлива | Неэтилированный |
| Диаметр и ход поршня, мм | 70,5/80 |
| Степень сжатия | 10,5 |
| ТРАНСМИССИЯ | |
| Тип привода | Передний |
| Коробка передач | Автоматический |
| Тип сцепления | Автоматический |
| ОБЪЕМЫ И МАССЫ | |
| Объем топливного бака, л | 35 |
| Объем багажника, л | 170(VDA) |
| Аккумулятор | 12V 50AH |
| Снаряженная масса автомобиля, кг | 1054 |
| Разрешенная максимальная масса, кг | 1365 |
| Генератор | 100A |
| ДИНАМИЧЕСКИЕ ХАРАКТЕРИСТИКИ | |
| Разгон до 100 км/ч с места, cекунд | 12,4 |
| Максимальная скорость, км/ч | 161 |
| ТОРМОЗНАЯ СИСТЕМА | |
| Передние тормоза | Дисковые |
| Задние тормоза | Барабанные |
| ПОДВЕСКА | |
| Передняя подвеска | Тип Макферсон |
| Задняя подвеска | Полузависимая, торсионная |
| Рулевое управление | Электрический |
| Шины | 155/70R14(R13) |
| Размер диска | 4. 5Jx14 5Jx14 |
| РАСХОД ТОПЛИВА (ЛИТР/100КМ) | |
| Смешанный цикл | 6,2 |
| Городской цикл | 8,2 |
Формула R-квадрата, регрессия и интерпретации
Что такое R-квадрат?
R-квадрат (R 2 ) — это статистическая мера, представляющая долю дисперсии зависимой переменной, которая объясняется независимой переменной или переменными в регрессионной модели. В то время как корреляция объясняет силу связи между независимой и зависимой переменной, R-квадрат объясняет, в какой степени дисперсия одной переменной объясняет дисперсию второй переменной. Итак, если R 2 модели равно 0,50, то примерно половина наблюдаемых изменений может быть объяснена входными данными модели.
Ключевые выводы
- R-квадрат — это статистическая мера соответствия, которая показывает, насколько вариации зависимой переменной объясняются независимыми переменными в регрессионной модели.
- В инвестировании R-квадрат обычно интерпретируется как процент движения фонда или ценной бумаги, который можно объяснить движениями эталонного индекса. 92 = 1 — \frac{ \text{Необъяснимая вариация} }{ \text{Общая вариация} } \\ \end{aligned}
R2=1 — Всего вариаций, необъяснимых вариаций
Фактический расчет R-квадрата требует нескольких шагов. Это включает в себя получение точек данных (наблюдений) зависимых и независимых переменных и поиск линии наилучшего соответствия, часто из регрессионной модели. Оттуда вы будете вычислять прогнозируемые значения, вычитать фактические значения и возводить результаты в квадрат. Это дает список ошибок в квадрате, который затем суммируется и равен необъяснимой дисперсии.
Чтобы вычислить общую дисперсию, вы должны вычесть среднее фактическое значение из каждого из фактических значений, возвести результаты в квадрат и просуммировать их.
 Отсюда разделите первую сумму ошибок (объясненная дисперсия) на вторую сумму (общая дисперсия), вычтите результат из единицы, и вы получите R-квадрат.
Отсюда разделите первую сумму ошибок (объясненная дисперсия) на вторую сумму (общая дисперсия), вычтите результат из единицы, и вы получите R-квадрат.Что R-квадрат может вам сказать
В инвестировании R-квадрат обычно интерпретируется как процент движения фонда или ценной бумаги, который можно объяснить движениями эталонного индекса. Например, R-квадрат для ценной бумаги с фиксированным доходом по сравнению с индексом облигаций определяет долю движения ценной бумаги, которая предсказуема на основе движения цены индекса.
То же самое можно применить к акции по сравнению с индексом S&P 500 или любым другим соответствующим индексом. Он также может быть известен как коэффициент детерминации.
Значения R-квадрата варьируются от 0 до 1 и обычно указываются в процентах от 0% до 100%. R-квадрат, равный 100%, означает, что все движения ценной бумаги (или другой зависимой переменной) полностью объясняются движениями индекса (или интересующей вас независимой переменной).

В инвестировании высокий R-квадрат, от 85 % до 100 %, указывает на то, что акции или показатели фонда движутся относительно в соответствии с индексом. Фонд с низким R-квадратом, на уровне 70% или меньше, указывает на то, что ценная бумага обычно не следует за движениями индекса. Более высокое значение R-квадрата будет указывать на более полезную бета-коэффициент. Например, если акции или фонды имеют значение R-квадрата, близкое к 100%, но бета ниже 1, они, скорее всего, предлагают более высокую доходность с поправкой на риск.
Сравнение R-квадрата со скорректированным R-квадратом
R-Squared работает должным образом только в простой модели линейной регрессии с одной независимой переменной. При множественной регрессии, состоящей из нескольких независимых переменных, R-квадрат необходимо корректировать.
Скорректированный R-квадрат сравнивает описательную силу регрессионных моделей, включающих различное количество предикторов. Каждый предиктор, добавленный в модель, увеличивает R-квадрат и никогда не уменьшает его.
 Таким образом, может показаться, что модель с большим количеством членов лучше подходит только потому, что в ней больше членов, в то время как скорректированный R-квадрат компенсирует добавление переменных и увеличивается только в том случае, если новый член улучшает модель по сравнению с тем, что было бы. получается по вероятности и уменьшается, когда предиктор улучшает модель меньше, чем предсказано случайно.
Таким образом, может показаться, что модель с большим количеством членов лучше подходит только потому, что в ней больше членов, в то время как скорректированный R-квадрат компенсирует добавление переменных и увеличивается только в том случае, если новый член улучшает модель по сравнению с тем, что было бы. получается по вероятности и уменьшается, когда предиктор улучшает модель меньше, чем предсказано случайно.В условии переобучения получается неправильно высокое значение R-квадрата, даже если модель фактически имеет пониженную способность прогнозировать. Это не относится к скорректированному R-квадрату.
R-квадрат против бета-версии
Бета и R-квадрат — это две связанные, но разные меры корреляции, но бета — это мера относительного риска. Взаимный фонд с высоким R-квадратом сильно коррелирует с эталоном. Если бета также высока, она может принести более высокую доходность, чем контрольный показатель, особенно на бычьих рынках. R-квадрат измеряет, насколько близко каждое изменение цены актива коррелирует с эталоном.

Бета измеряет, насколько велики эти изменения цен по сравнению с эталоном. При совместном использовании R-квадрат и бета дают инвесторам исчерпывающую картину эффективности управляющих активами. Бета, равная ровно 1,0, означает, что риск (волатильность) актива идентичен риску его эталона. По сути, R-квадрат — это метод статистического анализа для практического использования и проверки достоверности бета-коэффициентов ценных бумаг.
Ограничения R-Squared
R-квадрат даст вам оценку взаимосвязи между движениями зависимой переменной на основе движений независимой переменной. Он не говорит вам, хороша или плоха выбранная вами модель, и не говорит вам, являются ли данные и прогнозы предвзятыми. Высокий или низкий R-квадрат не обязательно является хорошим или плохим, поскольку он не говорит ни о надежности модели, ни о том, правильно ли вы выбрали регрессию. Вы можете получить низкий R-квадрат для хорошей модели или высокий R-квадрат для плохо подогнанной модели, и наоборот.

Что такое хорошее значение R-квадрата?
То, что считается «хорошим» значением R-квадрата, зависит от контекста. В некоторых областях, таких как социальные науки, даже относительно низкий R-квадрат, такой как 0,5, можно считать относительно сильным. В других областях стандарты хорошего чтения R-квадрата могут быть намного выше, например, 0,9 или выше. В финансах R-квадрат выше 0,7, как правило, указывает на высокий уровень корреляции, тогда как показатель ниже 0,4 указывает на низкую корреляцию. Однако это не жесткое правило, и оно будет зависеть от конкретного анализа.
Что означает значение R-квадрата 0,9?
По существу, значение R-квадрата, равное 0,9, указывает на то, что 90% дисперсии изучаемой зависимой переменной объясняется дисперсией независимой переменной. Например, если взаимный фонд имеет значение R-Squared 0,9 по отношению к его эталону, это будет означать, что 90% дисперсии фонда объясняется дисперсией его эталонного индекса.
Чем выше R-квадрат, тем лучше?
Здесь снова все зависит от контекста.
 Предположим, вы ищете индексный фонд, который будет максимально точно отслеживать конкретный индекс. В этом сценарии вы хотели бы, чтобы R-Squared фонда был как можно выше, поскольку его цель — соответствовать индексу, а не превышать его. С другой стороны, если вы ищете активно управляемые фонды, высокий R-квадрат может рассматриваться как плохой знак, указывающий на то, что управляющие фондами не добавляют достаточной ценности по сравнению с их контрольными показателями.
Предположим, вы ищете индексный фонд, который будет максимально точно отслеживать конкретный индекс. В этом сценарии вы хотели бы, чтобы R-Squared фонда был как можно выше, поскольку его цель — соответствовать индексу, а не превышать его. С другой стороны, если вы ищете активно управляемые фонды, высокий R-квадрат может рассматриваться как плохой знак, указывающий на то, что управляющие фондами не добавляют достаточной ценности по сравнению с их контрольными показателями.Как интерпретировать R-квадрат в регрессионном анализе
R-квадрат — это показатель согласия для моделей линейной регрессии. Эта статистика показывает процент дисперсии зависимой переменной, которую независимые переменные объясняют вместе. R-квадрат измеряет силу связи между вашей моделью и зависимой переменной по удобной шкале от 0 до 100 %.
После подбора модели линейной регрессии необходимо определить, насколько хорошо модель соответствует данным. Хорошо ли он объясняет изменения в зависимой переменной? Существует несколько ключевых статистических показателей согласия для регрессионного анализа.
 В этом посте мы рассмотрим R-квадрат (R 2 ), выделите некоторые его ограничения и обнаружите несколько сюрпризов. Например, малые значения R-квадрата не всегда являются проблемой, а высокие значения R-квадрата не обязательно хороши!
В этом посте мы рассмотрим R-квадрат (R 2 ), выделите некоторые его ограничения и обнаружите несколько сюрпризов. Например, малые значения R-квадрата не всегда являются проблемой, а высокие значения R-квадрата не обязательно хороши!Похожие сообщения : Когда я должен использовать регрессионный анализ? и Как выполнить регрессионный анализ с использованием Excel
Оценка согласия в регрессионной модели
Остатки — это расстояние между наблюдаемым значением и подобранным значением.Линейная регрессия определяет уравнение, которое дает наименьшую разницу между всеми наблюдаемыми значениями и их подобранными значениями. Чтобы быть точным, линейная регрессия находит наименьшую сумму квадратов остатков, возможную для набора данных.
Статистики говорят, что регрессионная модель хорошо соответствует данным, если различия между наблюдениями и прогнозируемыми значениями малы и беспристрастны.
 Беспристрастность в этом контексте означает, что подобранные значения не являются систематически слишком высокими или слишком низкими где-либо в пространстве наблюдения.
Беспристрастность в этом контексте означает, что подобранные значения не являются систематически слишком высокими или слишком низкими где-либо в пространстве наблюдения.Однако перед оценкой числовых показателей согласия, таких как R-квадрат, следует оценить остаточные графики. Графики остатков могут выявить предвзятую модель гораздо эффективнее, чем числовой вывод, поскольку отображают проблемные закономерности в остатках. Если ваша модель предвзята, вы не можете доверять результатам. Если ваши остаточные графики выглядят хорошо, продолжайте и оцените свой R-квадрат и другие статистические данные.
Прочтите мой пост о проверке остаточных участков.
R-квадрат и критерий согласия
R-квадрат оценивает разброс точек данных вокруг подобранной линии регрессии. Его также называют коэффициентом детерминации или коэффициентом множественной детерминации для множественной регрессии. Для одного и того же набора данных более высокие значения R-квадрата представляют меньшие различия между наблюдаемыми данными и подобранными значениями.

R-квадрат — это процентная доля вариации зависимой переменной, которую объясняет линейная модель.
R-квадрат всегда находится в диапазоне от 0 до 100 %:
- 0 % представляет собой модель, которая не объясняет каких-либо отклонений переменной отклика от ее среднего значения. Среднее значение зависимой переменной предсказывает зависимую переменную, а также модель регрессии.
- 100% представляет собой модель, которая объясняет все изменения переменной отклика вокруг ее среднего значения.
Обычно, чем больше R 2 , тем лучше регрессионная модель соответствует вашим наблюдениям. Однако у этого руководства есть важные оговорки, которые я буду обсуждать в этом и следующем постах.
Связанный пост : Что такое независимые и зависимые переменные?
Визуальное представление R-квадрата
Чтобы наглядно продемонстрировать, как значения R-квадрата представляют разброс вокруг линии регрессии, вы можете построить соответствующие значения по наблюдаемым значениям.

R-квадрат для регрессионной модели слева равен 15%, а для модели справа — 85%. Когда модель регрессии учитывает большую часть дисперсии, точки данных находятся ближе к линии регрессии. На практике вы никогда не увидите регрессионную модель с R 9.0005 2 100%. В этом случае подобранные значения равны значениям данных и, следовательно, все наблюдения попадают точно на линию регрессии.
R-квадрат имеет ограничения
Вы не можете использовать R-квадрат, чтобы определить, являются ли оценки коэффициентов и прогнозы смещенными, поэтому вы должны оценивать остаточные графики.
R-квадрат не показывает, обеспечивает ли регрессионная модель адекватное соответствие вашим данным. Хорошая модель может иметь низкую стоимость R 2 . С другой стороны, предвзятая модель может иметь высокий R 2 значение!
Всегда ли низкие значения R-квадрата являются проблемой?
Нет! Регрессионные модели с низкими значениями R-квадрата могут быть очень хорошими моделями по нескольким причинам.

Некоторым областям исследования присуще большее количество необъяснимых вариаций. В этих областях ваши значения R 2 должны быть ниже. Например, исследования, которые пытаются объяснить человеческое поведение, обычно имеют значения R 2 менее 50%. Просто людей труднее предсказать, чем такие вещи, как физические процессы.
К счастью, если у вас низкое значение R-квадрата, но независимые переменные статистически значимы, вы все равно можете сделать важные выводы о взаимосвязях между переменными. Статистически значимые коэффициенты продолжают представлять среднее изменение зависимой переменной при сдвиге независимой переменной на одну единицу. Очевидно, что иметь возможность делать такие выводы жизненно важно.
Связанный пост : Как интерпретировать регрессионные модели со значимыми переменными, но с низким R-квадратом
Существует сценарий, при котором малые значения R-квадрата могут вызвать проблемы. Если вам нужно генерировать прогнозы, которые являются относительно точными (узкие интервалы прогнозирования), низкий R 2 может оказаться решающим фактором.

Насколько высоким должен быть R-квадрат, чтобы модель давала полезные прогнозы? Это зависит от требуемой точности и количества вариаций, присутствующих в ваших данных. Высокое значение R 2 необходимо для точных прогнозов, но одного этого недостаточно, как мы узнаем в следующем разделе.
Похожие сообщения : Понимание точности в прикладной регрессии, чтобы избежать дорогостоящих ошибок и среднеквадратичной ошибки (MSE)
Всегда ли высокие значения R-квадрата хороши?
Нет! Модель регрессии с высоким значением R-квадрата может иметь множество проблем. Вы, вероятно, ожидаете, что высокое значение R 2 указывает на хорошую модель, но изучите графики ниже. Подогнанный линейный график моделирует связь между подвижностью электронов и плотностью.
Данные на аппроксимированном линейном графике следуют очень низкому шумовому соотношению, а R-квадрат составляет 98,5%, что кажется фантастическим. Однако линия регрессии постоянно занижает и завышает данные вдоль кривой, что является смещением.
 График «Остатки против подгонки» подчеркивает эту нежелательную закономерность. Несмещенная модель имеет остатки, которые случайным образом разбросаны вокруг нуля. Неслучайные остаточные паттерны указывают на плохое соответствие, несмотря на высокое значение R 2 . Всегда проверяйте остаточные участки!
График «Остатки против подгонки» подчеркивает эту нежелательную закономерность. Несмещенная модель имеет остатки, которые случайным образом разбросаны вокруг нуля. Неслучайные остаточные паттерны указывают на плохое соответствие, несмотря на высокое значение R 2 . Всегда проверяйте остаточные участки!Этот тип смещения спецификации возникает, когда ваша линейная модель занижена. Другими словами, в нем отсутствуют значимые независимые переменные, полиномиальные члены и условия взаимодействия. Чтобы произвести случайные остатки, попробуйте добавить члены в модель или подобрать нелинейную модель.
Связанный пост : Спецификация модели: Выбор правильной регрессионной модели
Ряд других обстоятельств может искусственно завышать ваш R 2 . Эти причины включают переоснащение модели и интеллектуальный анализ данных. Любой из них может создать модель, которая выглядит так, как будто она обеспечивает отличное соответствие данным, но на самом деле результаты могут быть полностью обманчивыми.

Модель переобучения — это модель, в которой модель соответствует случайным особенностям выборки. Интеллектуальный анализ данных может использовать случайные корреляции. В любом случае вы можете получить модель с высоким R 2 даже для совершенно случайных данных!
Связанный пост : Пять причин, почему ваш R-квадрат может быть слишком высоким
R-квадрат не всегда прямолинеен соответствует набору данных. Тем не менее, это не говорит нам всей истории. Для получения полной картины необходимо учитывать R
2 значений в сочетании с остаточными графиками, другими статистическими данными и глубоким знанием предметной области.В следующем посте я продолжу изучение ограничений R 2 и рассмотрю два других типа R 2 : скорректированный R-квадрат и прогнозируемый R-квадрат. Эти две статистики решают конкретные проблемы с R-квадратом. Они предоставляют дополнительную информацию, с помощью которой вы можете оценить соответствие вашей регрессионной модели.

Вы также можете прочитать о стандартной ошибке регрессии, которая представляет собой другой тип меры согласия.
Обязательно прочтите мой пост, где я отвечаю на извечный вопрос: Насколько высоким должен быть R-квадрат?
Если вы изучаете регрессию и вам нравится подход, который я использую в своем блоге, ознакомьтесь с моей книгой «Интуитивное руководство по регрессионному анализу»! Вы можете найти его на Amazon и других розничных магазинах.
Примечание. Я написал другую версию этого поста, которая появилась в другом месте. Я полностью переписал и обновил его для своего блога.
2.5 — Коэффициент детерминации, r-квадрат
Давайте начнем исследование коэффициента детерминации r 2 с двух разных примеров: один пример, в котором связь между ответом y и предиктором x очень слабая, а второй пример, в котором связь между ответом y и предиктором х довольно сильна.
 Если наша мера будет работать хорошо, она должна уметь различать эти две совершенно разные ситуации.
Если наша мера будет работать хорошо, она должна уметь различать эти две совершенно разные ситуации.Вот график, иллюстрирующий очень слабую связь между y и x . На графике есть две линии: горизонтальная линия, расположенная на среднем ответе, \(\bar{y}\), и пологая предполагаемая линия регрессии, \(\hat{y}\). Обратите внимание, что наклон оценочной линии регрессии не очень крутой, что позволяет предположить, что по мере увеличения предиктора x средний ответ y изменяется незначительно. Также обратите внимание, что точки данных не «обнимают» предполагаемую линию регрессии: 92=1827,6\)
Расчеты в правой части графика показывают противоположные значения «суммы квадратов»:
- SSR представляет собой «сумму квадратов регрессии» и количественно определяет, насколько далеко наклонена предполагаемая линия регрессии, \(\hat{y} _i\), берется из горизонтальной «линии отсутствия связи», среднего значения выборки или \(\bar{y}\).

- SSE представляет собой «сумму квадратов ошибок» и количественно определяет, насколько точки данных, \(y_i\), варьируются вокруг оценочной линии регрессии, \(\hat{y}_i\).
- SSTO представляет собой «общую сумму квадратов» и количественно определяет, насколько точки данных, \(y_i\), отличаются от своего среднего значения, \(\bar{y}\).
Обратите внимание, что SSTO = SSR + SSE. Суммы квадратов, кажется, довольно хорошо рассказывают историю. Они говорят нам, что большая часть вариаций отклика 90 218 y 90 221 (90 218 SSTO 90 221 = 1827,6) обусловлена случайными вариациями (90 218 SSE 90 221 = 1708,5), а не регрессией 90 218 y 90 221 на 90 218 x 90 221 ( 90 218 ССР = 119.1). Вы могли заметить, что SSR , разделенное на SSTO , равно 119,1/1827,6 или 0,065. Вы видите, где эта величина появляется на приведенном выше графике?
Сравните приведенный выше пример со следующим, в котором график иллюстрирует довольно убедительную связь между y и x .
 Наклон оценочной линии регрессии намного круче, что позволяет предположить, что по мере увеличения предиктора x происходит довольно существенное изменение (уменьшение) отклика 92=8487,8\)
Наклон оценочной линии регрессии намного круче, что позволяет предположить, что по мере увеличения предиктора x происходит довольно существенное изменение (уменьшение) отклика 92=8487,8\)Сумма квадратов для этого набора данных говорит совсем о другом, а именно о том, что большая часть вариации отклика y ( SSTO = 8487,8) связана с регрессией y на x ( SSR = 6679,3) не только из-за случайной ошибки ( SSE = 1708,5). А SSR , деленное на SSTO , равно 6679,3/8487,8 или 0,799, что снова появляется на построенном графике.
В предыдущих двух примерах было предложено формальное определение меры. Короче говоря, «коэффициент детерминации » или « r — значение в квадрате », обозначаемое как r 2 , представляет собой сумму квадратов регрессии, деленную на общую сумму квадратов. В качестве альтернативы, как показано в этом скриншоте ниже, поскольку SSTO = SSR + SSE , количество r 2 также равно единице минус отношение суммы квадратов ошибок к общей сумме квадратов: 92=\frac{SSR}{SSTO}=1-\frac{SSE}{SSTO}\]
youtube.com/embed/bkoqUimGOgM?rel=0″ frameborder=»0″ webkitallowfullscreen=»webkitallowfullscreen» allowfullscreen=»allowfullscreen» mozallowfullscreen=»mozallowfullscreen»>Вот некоторые основные характеристики меры:
- это всегда число от 0 до 1.
- Если r 2 = 1, все точки данных точно попадают на линию регрессии. Предсказатель x учитывает все вариации y !
- Если р 2 = 0 расчетная линия регрессии совершенно горизонтальна. Предсказатель x учитывает ни одного вариации y !
Мы выучили интерпретацию для двух простых случаев — когда r 2 = 0 или r 2 = 1 — но как мы интерпретируем r 2 , когда это некоторое число между 0 и 1, например, 0,23 или 0,57, скажем? Вот два похожих, но несколько разных способа определения коэффициента детерминации 9.
 0218 r 2 можно интерпретировать. Мы говорим либо:
0218 r 2 можно интерпретировать. Мы говорим либо:« R 2 × 100 процентов от вариации в Y снижается, принимая во внимание предиктор x »
или:
« R 2 .
» R
2 . вариации y «объясняется» вариацией предиктора x .Многие статистики предпочитают первую интерпретацию. Я склоняюсь ко второму. Риск использования второй интерпретации — и, следовательно, почему «объясняется» взято в кавычки, — заключается в том, что ее можно неправильно истолковать как предполагающую, что предиктор x вызывает изменение ответа y . Ассоциация не является причинно-следственной связью. То есть только потому, что набор данных характеризуется большим значением 90 218 r 90 221 в квадрате, это не означает, что 90 218 x 90 221 90 218 вызывает 90 221 изменения в 90 218 y 90 221 . Пока вы держите в уме правильное значение, можно использовать вторую интерпретацию.
 Вариант второй интерпретации состоит в том, чтобы сказать: « r 2 × 100 процентов вариации в y объясняется изменением предиктора x ».
Вариант второй интерпретации состоит в том, чтобы сказать: « r 2 × 100 процентов вариации в y объясняется изменением предиктора x ».Студенты часто спрашивают: «Что считается большим значением r в квадрате?» Это зависит от области исследования. Социологи, которые часто пытаются учиться что-то в огромной изменчивости человеческого поведения будет иметь тенденцию к тому, что будет очень трудно получить значения r -квадрат намного выше, скажем, 25% или 30% Инженеры, с другой стороны, которые склонны изучать более точные системы, скорее всего, найдут r — значение в квадрате всего 30% неприемлемо. Мораль этой истории заключается в том, чтобы прочитать литературу, чтобы узнать, какие типичные значения r -квадрат для вашей области исследований!
Вернемся к примеру со смертностью от рака кожи (skincancer.txt). Любое статистическое программное обеспечение, выполняющее простой линейный регрессионный анализ, сообщит вам значение r -квадрат, которое в данном случае составляет 67,98% или 68% до ближайшего целого числа.

Мы можем сказать, что 68% вариации уровня смертности от рака кожи уменьшается за счет учета широты. Или, зная, что это на самом деле означает, мы можем сказать, что 68% вариаций смертности от рака кожи «объясняется» широтой.
‹ 2.4 — Что такое дисперсия общей ошибки? вверх 2.6 — Коэффициент корреляции (Пирсона) r ›
Как интерпретировать R-квадрат в регрессионном анализе?
Регрессионный анализ — это набор статистических процессов, лежащих в основе науки о данных. В области численного моделирования он представляет наиболее понятные модели и помогает интерпретировать алгоритмы машинного обучения. Их реальное применение можно увидеть в самых разных областях, от рекламы и медицинских исследований до сельскохозяйственной науки и даже различных видов спорта. В моделях линейной регрессии интерпретация r в квадрате является мерой соответствия. Он учитывает силу связи между моделью и зависимой переменной. Его удобство измеряется по шкале от 0 до 100%.

Когда у вас есть подходящая модель линейной регрессии, вам необходимо решить несколько вопросов:
- Насколько хорошо модель соответствует данным?
- Насколько хорошо это объясняет изменения зависимой переменной?
В этой статье мы узнаем о R-квадрате (R 2 ), интерпретации r-квадрата, ограничениях и нескольких разных идеях о нем. Мы также рассмотрим машинное обучение с основами Python и многое другое.
Давайте сначала поймем основы регрессионного анализа и его необходимость.
Что такое регрессионный анализ?
Регрессионный анализ — это хорошо известный метод статистического обучения, который позволяет вам исследовать взаимосвязь между независимыми переменными (или независимыми переменными) и зависимыми переменными (или переменными реакции). Это требует, чтобы вы сформулировали математическую модель, которую можно использовать для определения оценочного значения, которое почти близко к фактическому значению.

Два термина, необходимые для понимания регрессионного анализа:
- Зависимые переменные – факторы, которые вы хотите понять или предсказать.
- Независимые переменные — факторы, влияющие на зависимую переменную.
Рассмотрим ситуацию, когда вам даны данные о группе студентов по определенным факторам: количество часов обучения в день, посещаемость и баллы на конкретном экзамене. Техника регрессии позволяет выявить наиболее существенные факторы, факторы, которыми можно пренебречь, и зависимость одних факторов от других.
Метод регрессионного анализа в основном преследует две цели:
- Объяснительный анализ. Этот анализ позволяет понять и определить влияние объясняющей переменной на переменную отклика в отношении определенной модели.
- Прогнозный анализ. Этот анализ используется для прогнозирования значения, предполагаемого зависимой переменной.
Зачем использовать регрессионный анализ?
Метод генерирует уравнение регрессии, в котором взаимосвязь между независимой переменной и переменной отклика представлена параметрами метода.

Вы можете использовать регрессионный анализ для выполнения следующих действий:
- Для моделирования различных независимых переменных.
- Для добавления непрерывных и категориальных переменных, имеющих многочисленные отдельные группы на основе характеристики.
- Для моделирования кривизны с использованием полиномиальных членов.
- Для определения влияния одной независимой переменной на другую переменную путем оценки условий взаимодействия.
Что такое остатки?
Остатки определяют отклонение наблюдаемых значений от ожидаемых значений. Их также называют ошибками или помехами. Остаток дает представление о том, насколько хороша наша модель по сравнению с фактическим значением, но нет реальных представлений остаточных значений.
Источник: hatarilabs.com
Линия регрессии и графики остатков
Вычисление реальных значений точек пересечения, наклона и остатков может быть сложной задачей. Однако метод регрессии с обычными наименьшими квадратами (OLS) может помочь нам построить эффективную модель.
 Метод минимизирует сумму квадратов остатков. С помощью графиков остатков можно проверить, согласуется ли наблюдаемая ошибка со стохастической ошибкой (различия между ожидаемыми и наблюдаемыми значениями должны быть случайными и непредсказуемыми).
Метод минимизирует сумму квадратов остатков. С помощью графиков остатков можно проверить, согласуется ли наблюдаемая ошибка со стохастической ошибкой (различия между ожидаемыми и наблюдаемыми значениями должны быть случайными и непредсказуемыми).Что такое Goodness-of-Fit?
Регрессионный анализ является частью метода линейной регрессии. Он исследует уравнение, которое уменьшает расстояние между подобранной линией и всеми точками данных. Определение того, насколько хорошо модель соответствует данным, имеет решающее значение в линейной модели.
Общая идея заключается в том, что если отклонения между наблюдаемыми значениями и прогнозируемыми значениями линейной модели малы и несмещены, модель имеет хорошо подобранные данные.
С технической точки зрения, «добросоответствие» – это математическая модель, описывающая различия между наблюдаемыми значениями и ожидаемыми значениями или то, насколько хорошо модель соответствует набору наблюдений. Эта мера может быть использована при проверке статистической гипотезы.

Как оценить соответствие регрессионной модели?
По мнению статистиков, если различия между наблюдениями и прогнозируемыми значениями небольшие и непредвзятые, можно сказать, что модель хорошо соответствует данным. Смысл несмещенности в данном контексте заключается в том, что подобранные значения не достигают крайних значений, т.е. слишком высоких или слишком низких во время наблюдений.
Как мы видели ранее, модель линейной регрессии дает вам представление об уравнении, которое представляет минимальную разницу между наблюдаемыми значениями и прогнозируемыми значениями. Проще говоря, мы можем сказать, что линейная регрессия r в квадрате определяет наименьшую сумму квадратов остатков, вероятных для набора данных.
Определение остаточных графиков представляет собой важную часть регрессионной модели, и его следует выполнять перед оценкой числовых показателей согласия, таких как R-квадрат. Они помогают распознать предвзятую модель, выявляя проблемные закономерности на остаточных графиках.

Однако, если у вас предвзятая модель, вы не можете полагаться на результаты. Если остаточные графики выглядят хорошо, вы можете оценить значение R-квадрата и другие числовые результаты. Если вы новичок и эти концепции кажутся вам сложными, запишитесь на наш курс по науке о данных и начните с нуля по собственному графику.
Что такое R-квадрат? Значение
R в квадрате (R 2 ) в машинном обучении называется коэффициентом детерминации или коэффициентом множественной детерминации в случае множественной регрессии.
Квадрат R в регрессии действует как показатель оценки для оценки разброса точек данных вокруг подобранной линии регрессии. Он распознает процент вариации зависимой переменной.
R-квадрат и критерий согласия
R-квадрат — это доля дисперсии зависимой переменной, которая может быть объяснена независимой переменной.
Значение R-квадрата остается между 0 и 100 %:
- 0 % соответствует модели, которая не объясняет изменчивость данных отклика вокруг своего среднего значения.
 Среднее значение зависимой переменной помогает предсказать зависимую переменную, а также модель регрессии.
Среднее значение зависимой переменной помогает предсказать зависимую переменную, а также модель регрессии. - С другой стороны, 100% соответствует модели, которая объясняет изменчивость переменной отклика вокруг ее среднего значения.
Если ваше значение R 2 большое, у вас больше шансов, что ваша регрессионная модель будет соответствовать наблюдениям.
Хотя вы можете получить важные сведения о регрессионной модели с помощью этой статистической меры, вы не должны полагаться на нее для полной оценки модели. Он не дает информации о взаимосвязи между зависимой и независимой переменными.
Также не информирует о качестве регрессионной модели. Следовательно, как пользователь, вы всегда должны анализировать R 2 вместе с другими переменными, а затем сделайте выводы о регрессионной модели.
Визуальное представление R-квадрата
Вы можете графически продемонстрировать графики подобранных значений по наблюдаемым значениям.
 Он иллюстрирует, как значения R-квадрата представляют разброс вокруг линии регрессии.
Он иллюстрирует, как значения R-квадрата представляют разброс вокруг линии регрессии.Как видно на рисунках выше, значение R-квадрата для регрессионной модели слева составляет 17%, а для модели справа — 83%. В регрессионной модели, когда учитывается высокая дисперсия, точки данных имеют тенденцию приближаться к подобранной линии регрессии.
Однако регрессионная модель с R 2 100 % является идеальным сценарием, который на самом деле невозможен. В таком случае прогнозируемые значения равны наблюдаемым значениям, и это приводит к тому, что все точки данных попадают точно на линию регрессии.
Как интерпретировать R в квадрате
Простейшая интерпретация r в квадрате заключается в том, насколько хорошо модель регрессии соответствует наблюдаемым значениям данных. Давайте возьмем пример, чтобы понять это.
Рассмотрим модель, в которой R 2 значение равно 70%. Здесь r в квадрате означает, что модель объясняет 70% подогнанных данных в регрессионной модели.
 Обычно, когда значение R 2 высокое, это предполагает лучшее соответствие модели.
Обычно, когда значение R 2 высокое, это предполагает лучшее соответствие модели.Правильность статистической меры зависит не только от R 2 , но может зависеть от нескольких других факторов, таких как характер переменных, единицы измерения переменных и т. д. Таким образом, высокое значение R-квадрата не всегда вероятен для регрессионной модели и также может указывать на проблемы.
Низкое значение R-квадрата является отрицательным показателем для модели в целом. Однако, если мы рассмотрим другие факторы, низкое значение R 2 также может оказаться хорошей прогностической моделью.
Расчет R-квадрата
R-квадрата можно рассчитать по следующей формуле:
Где:
- SS-регрессия – Объясненная сумма квадратов в соответствии с регрессионной моделью.
- SStotal — общая сумма квадратов.
Сумма квадратов из-за регрессии оценивает, насколько хорошо модель представляет подобранные данные, а общая сумма квадратов измеряет изменчивость данных, используемых в регрессионной модели.

Теперь давайте вернемся к более ранней ситуации, когда у нас есть два фактора: количество часов обучения в день и оценка на конкретном экзамене, чтобы лучше понять расчет R-квадрата. Здесь целевая переменная представлена баллом, а независимая переменная – количеством часов обучения в день.
В этом случае нам понадобится простая модель линейной регрессии, и уравнение модели будет следующим:
ŷ = w1x1 + b
Параметры w1 и b можно рассчитать путем уменьшения квадрата ошибки по всем точки данных. Следующее уравнение называется функцией наименьших квадратов:
минимизировать ∑(yi – w1x1i – b) 2
Теперь, чтобы вычислить согласие, нам нужно вычислить дисперсию:
var(u) = 1/n∑(ui – ū) 2
где n представляет количество точек данных.
Теперь R-квадрат вычисляет величину дисперсии целевой переменной, объясненной моделью, т. е. функцию независимой переменной.
Однако для этого нам нужно рассчитать две вещи:
- Дисперсия целевой переменной:
var(avg) = ∑(yi – Ӯ) 2
- Дисперсия целевой переменной вокруг линии наилучшего соответствия:
var(model) = ∑ yi – ŷ) 2
Наконец, мы можем рассчитать уравнение R-квадрата следующим образом: – ŷ) 2 /∑(yi – Ӯ) 2 ]
Ограничения R-квадрата
Некоторые из ограничений R-квадрата:
- R-квадрат нельзя использовать для проверки того, являются ли оценки коэффициентов и прогнозы смещенными или нет.

- R-квадрат не сообщает, адекватна ли модель регрессии или нет.
Чтобы определить смещение модели, необходимо оценить графики остатков. У хорошей модели может быть низкое значение R-квадрата, тогда как у модели, которая не имеет надлежащего согласия, может быть высокое значение R-квадрата.
Низкие и высокие значения R-квадрата
Регрессионные модели с низким R 2 не всегда создают проблемы. В некоторых областях у вас обязательно будут низкие значения R 2 . Один из таких случаев — когда вы изучаете человеческое поведение. Они, как правило, имеют R 2 значения менее 50%. Причина этого в том, что предсказание людей — более сложная задача, чем предсказание физического процесса.
Вы можете сделать важные выводы о том, что ваша модель имеет низкое значение R 2 , когда независимые переменные модели имеют некоторую статистическую значимость. Они представляют собой среднее изменение зависимой переменной, когда независимая переменная смещается на одну единицу.

Однако, если вы работаете над моделью для создания точных прогнозов, низкие значения R-квадрата могут вызвать проблемы.
Теперь давайте посмотрим на другую сторону медали. Модель регрессии с высоким значением R 2 может привести, как это называют статистики, к смещению спецификации. Этот тип ситуации возникает, когда линейная модель недоопределена из-за отсутствия важных независимых переменных, полиномиальных членов и членов взаимодействия.
Чтобы преодолеть эту ситуацию, вы можете создавать случайные остатки, добавляя соответствующие члены или подбирая нелинейную модель.
Методы переобучения модели и интеллектуального анализа данных также могут привести к завышению стоимости R 2 . Модель, которую они создают, может обеспечить отличное соответствие данным, но на самом деле результаты, как правило, полностью обманчивы.
ЗаключениеПодведем итог тому, что мы уже рассмотрели в этой статье:
- Регрессионный анализ и его значение , Расчет, Ограничения
- Низкий и высокий R 2 значения
Хотя R-квадрат является очень интуитивно понятным показателем, позволяющим определить, насколько хорошо регрессионная модель соответствует набору данных, он не дает полной картины.
 Если вы хотите получить полную картину, вам необходимо иметь глубокие знания R 2 наряду с другим статистическим анализом и остаточными графиками.
Если вы хотите получить полную картину, вам необходимо иметь глубокие знания R 2 наряду с другим статистическим анализом и остаточными графиками.Чтобы получить дополнительную информацию об ограничениях R-квадрата, вы можете узнать о скорректированной интерпретации r-квадрата и прогнозируемом R-квадрате , которые предоставляют различные сведения для оценки соответствия модели. Вы также можете взглянуть на другой тип меры согласия, например, на стандартную ошибку регрессии. Узнайте больше о приложениях линейной регрессии с помощью машинного обучения Knowledgehut с Python и других связанных курсов.
Среднеквадратическая ошибка и показатель R2 — ясное объяснение — программное обеспечение BMC
Сегодня мы познакомим вас с некоторыми терминами, важными для машинного обучения: концепции с использованием scikit-learn.
(Эта статья является частью нашего руководства по обучению scikit. Используйте правое меню для навигации.
 )
) Почему эти термины важны
Вам необходимо понимать эти показатели, чтобы определить, являются ли регрессионные модели точными или вводящие в заблуждение. Следовать ошибочной модели — плохая идея, поэтому важно, чтобы вы могли количественно оценить, насколько точна ваша модель. Понять это не так просто.
Эти первые показатели — лишь некоторые из них. Другие концепции, такие как смещение и переобучение моделей, также приводят к вводящим в заблуждение результатам и неверным прогнозам.
(Подробнее см. в разделе Смещение и дисперсия в машинном обучении.)
Чтобы привести примеры, давайте воспользуемся кодом из нашего последнего сообщения в блоге и добавим дополнительную логику. Мы также введем некоторую случайность в зависимую переменную ( y ), чтобы в наших прогнозах была некоторая ошибка. (Напомним, что в предыдущем посте мы сделали независимые y и зависимые переменные x прекрасно коррелируют, чтобы проиллюстрировать основы выполнения линейной регрессии с помощью scikit-learn.
 )
)Что такое дисперсия?
С точки зрения линейной регрессии, дисперсия является мерой того, насколько наблюдаемые значения отличаются от среднего значения прогнозируемых значений, т. е. их отличие от среднего прогнозируемого значения . Цель состоит в том, чтобы иметь низкое значение. То, что означает низкий , количественно определяется показателем r2 (поясняется ниже).
В приведенном ниже коде это np.var(err) , где err — это массив различий между наблюдаемыми и прогнозируемыми значениями, а np.var() — это функция дисперсии массива numpy.
Что такое оценка r2?
Оценка r2 варьируется от 0 до 100%. Он тесно связан с MSE (см. ниже), но не совпадает. Википедия определяет r2 как
«…доля дисперсии зависимой переменной, которую можно предсказать по независимой переменной (переменным)».

Другое определение: «(общая дисперсия, объясненная моделью) / общая дисперсия». Так что, если это 100%, две переменные идеально коррелированы, то есть вообще не имеют дисперсии. Низкое значение будет показывать низкий уровень корреляции, что означает, что модель регрессии недействительна, но не во всех случаях.
Читая приведенный ниже код, мы делаем это вычисление в три шага, чтобы его было легче понять. г — это сумма различий между наблюдаемыми и предсказанными значениями. (ytest[i] – pres[i]) **2 . y — каждое наблюдаемое значение y[i] минус среднее наблюдаемых значений np.mean(ytest) . И затем результаты печатаются следующим образом:
print ("общая сумма квадратов", y) print ("ẗобщая сумма остатков", г) print("r2 вычислено", 1 - (g/y))Наша цель здесь объяснить. Мы, конечно, можем позволить scikit изучить это с помощью метода r2_score():
print("Оценка R2: %. 2f" % r2_score(ytest,preds))
2f" % r2_score(ytest,preds)) Что такое среднеквадратическая ошибка (MSE)?
Среднеквадратическая ошибка (MSE) — это среднее квадратов ошибок. Чем больше число, тем больше ошибка. Ошибка в данном случае означает разницу между наблюдаемыми значениями y1, y2, y3, … и прогнозируемыми значениями pred(y1), pred(y2), pred(y3), … Возводим в квадрат каждую разницу (pred(yn) – yn)) ** 2, чтобы отрицательные и положительные значения не компенсировали друг друга.
Полный код
Вот полный код:
импортировать matplotlib.pyplot как plt из sklearn импортировать linear_model импортировать numpy как np из sklearn.metrics импорта mean_squared_error, r2_score reg = linear_model.LinearRegression() ar = np.array([[[1],[2],[3]], [[2.01],[4.03],[6.04]]]) у = ар[1,:] х = ар[0,:] reg.fit(x,y) print('Коэффициенты: \n', reg.coef_) xTest = np.массив([[4],[5],[6]]) ytest = np.массив([[9],[8.5],[14]]) preds = reg.predict(xTest) print("Оценка R2: %. 2f" % r2_score(ytest,preds))
print("Среднеквадратическая ошибка: %.2f" % mean_squared_error(ytest,preds))
э = []
г = 0
для i в диапазоне (len (ytest)):
print("actual=", ytest[i], "observed=", preds[i])
х = (ytest[i] - preds[i]) **2
э.добавить(х)
г = г + х
х = 0
для i в диапазоне (len (er)):
х = х + эр[я]
печать ("MSE", x/len(er))
v = np.var(er)
печать ("дисперсия", v)
печать ("среднее значение ошибок", np.mean(er))
m = np.mean (ytest)
print("среднее из наблюдаемых значений", м)
у = 0
для i в диапазоне (len (ytest)):
y = y + ((ytest[i] - m) ** 2)
print ("общая сумма квадратов", y)
print ("ẗобщая сумма остатков", г)
print("r2 вычислено", 1 - (g/y))
2f" % r2_score(ytest,preds))
print("Среднеквадратическая ошибка: %.2f" % mean_squared_error(ytest,preds))
э = []
г = 0
для i в диапазоне (len (ytest)):
print("actual=", ytest[i], "observed=", preds[i])
х = (ytest[i] - preds[i]) **2
э.добавить(х)
г = г + х
х = 0
для i в диапазоне (len (er)):
х = х + эр[я]
печать ("MSE", x/len(er))
v = np.var(er)
печать ("дисперсия", v)
печать ("среднее значение ошибок", np.mean(er))
m = np.mean (ytest)
print("среднее из наблюдаемых значений", м)
у = 0
для i в диапазоне (len (ytest)):
y = y + ((ytest[i] - m) ** 2)
print ("общая сумма квадратов", y)
print ("ẗобщая сумма остатков", г)
print("r2 вычислено", 1 - (g/y)) Результат:
Коэффициенты: [[2.015]] Оценка R2: 0,62 Среднеквадратическая ошибка: 2,34 факт = [9.] наблюдаемый = [8.05666667] факт = [8,5] наблюдаемый = [10,07166667] факт = [14.] наблюдаемый = [12.08666667] МСЭ [2.34028611] дисперсия 1,2881398892129619 среднее число ошибок 2,3402861111111117 среднее наблюдаемых значений 10,5 общая сумма квадратов [18,5] ẗобщая сумма остатков [7.
 02085833]
r2 вычислено [0,62049414]
02085833]
r2 вычислено [0,62049414] Вы можете увидеть, взглянув на данные np.array([[[1],[2],[3]], [[2.01],[4.03],[6.04]]]) что каждая зависимая переменная примерно в два раза больше независимой. Это подтверждается тем, что расчетный коэффициент reg.coef_ равен 2,015.
Нет правильного значения для MSE . Проще говоря, чем ниже значение, тем лучше, а 0 означает, что модель идеальна. Поскольку правильного ответа нет, основная ценность MSE заключается в выборе одной модели прогнозирования над другой.
Точно так же нет правильного ответа и на то, что R2 должен быть. 100% означает идеальную корреляцию. Тем не менее, есть модели с низким R2, которые по-прежнему являются хорошими моделями.
Наш вывод заключается в том, что вы не можете рассматривать эти показатели изолированно при оценке вашей модели. Вы должны смотреть и на другие показатели, а также понимать лежащую в их основе математику.
 Обо всем этом мы поговорим в следующих статьях блога.
Обо всем этом мы поговорим в следующих статьях блога.Дополнительные ресурсы
Расширение R-квадрата за пределы обычной линейной регрессии наименьших квадратов от pcdjohnson
Эти сообщения являются моими собственными и не обязательно отражают позицию, стратегию или мнение BMC.
Видите ошибку или есть предложение? Пожалуйста, сообщите нам об этом по электронной почте [email protected].
scikit Учебное руководство
Часто задаваемые вопросы: что такое псевдоR-квадраты?
Часто задаваемые вопросы: Что такое псевдоR-квадраты?
В качестве отправной точки напомним, что непсевдоR-квадрат — это статистика, полученная с помощью обычной регрессии методом наименьших квадратов (OLS), которая часто используется в качестве меры согласия. В ОЛС,
где N количество наблюдений в модели y — зависимая переменная, y -bar является средним значением y значений, а y -hat является значением предсказывает модель.
 Числитель отношения равен сумме квадратов
различия между фактическими значениями y и предсказанными y ценности. Знаменатель отношения представляет собой сумму квадратов разностей
между фактическим и значения и их среднее значение.
Числитель отношения равен сумме квадратов
различия между фактическими значениями y и предсказанными y ценности. Знаменатель отношения представляет собой сумму квадратов разностей
между фактическим и значения и их среднее значение.Есть несколько подходов к мышлению о R-квадрат в OLS. Эти разные подходы приводят к различные расчеты псевдо R-квадратов с регрессиями категориального результата переменные.
- R-квадрат как объясненная изменчивость –
Знаменатель отношения можно рассматривать как общую изменчивость в
зависимая переменная, или насколько y отличается от своего среднего значения.
числитель отношения можно рассматривать как изменчивость зависимой
переменная, которая не предсказывается моделью. Таким образом, это соотношение равно
доля общей изменчивости, необъяснимой моделью.
Вычитание этого отношения из единицы дает долю общего
изменчивость, объясняемая моделью. Чем больше объясняется изменчивость,
тем лучше модель.

- R-квадрат как улучшение от нуля модель к установленной модели – Можно подумать о знаменателе отношения как сумма квадратов ошибок нулевой модели — модели, предсказывающей зависимая переменная без каких-либо независимых переменных. В нуле модели, каждое значение y прогнозируется как среднее значение y ценности. Представьте себе, что вас попросили предсказать значение y без каких-либо дополнительную информацию о том, что вы прогнозируете. Среднее значение 9Значения 0904 и будут вашим лучшим предположением, если вы хотите минимизировать квадрат разницы между вашим прогнозом и фактическим значением y . Тогда числитель отношения будет суммой квадратов ошибок приталенная модель. Отношение указывает на степень, в которой модель параметры улучшают предсказание нулевой модели. Чем меньше это отношение, тем больше улучшение и выше R-квадрат.
- R-квадрат как квадрат
корреляция — Термин «R-квадрат» происходит от этого определения.
 R-квадрат — это квадрат корреляции между предсказанными моделью
значения и фактические значения. Эта корреляция может варьироваться от -1 до 1,
поэтому квадрат корреляции колеблется от 0 до 1.
большая величина корреляции
между прогнозируемыми значениями и фактическими значениями, тем больше
R-квадрат, независимо от того, является ли корреляция положительной или отрицательной.
R-квадрат — это квадрат корреляции между предсказанными моделью
значения и фактические значения. Эта корреляция может варьироваться от -1 до 1,
поэтому квадрат корреляции колеблется от 0 до 1.
большая величина корреляции
между прогнозируемыми значениями и фактическими значениями, тем больше
R-квадрат, независимо от того, является ли корреляция положительной или отрицательной.
При анализе данных с помощью логистического регрессии, эквивалентной статистики для R-квадрата не существует. Модель оценки из логистической регрессии — это оценки максимального правдоподобия, полученные через итеративный процесс. Они не рассчитаны на минимизацию дисперсия, поэтому подход МНК к оценке согласия неприменим. Однако, чтобы оценить соответствие логистических моделей, несколько псевдо-R-квадратов были разработаны. Это «псевдо» R-квадраты, потому что они выглядят как R-квадрат в том смысле, что они находятся в одинаковой шкале, начиная от 0 к 1 (хотя некоторые псевдоR-квадраты никогда не достигают 0 или 1) с более высокими значениями, указывающими на лучшее соответствие модели, но они не могут быть интерпретируется так, как можно было бы интерпретировать R-квадрат OLS, и различные псевдо R-квадраты могут прийти к очень разные ценности.
 Обратите внимание, что большинство программных пакетов сообщают натуральный логарифм
вероятность из-за проблем с точностью с плавающей запятой, которые чаще возникают с необработанными правдоподобиями.
Обратите внимание, что большинство программных пакетов сообщают натуральный логарифм
вероятность из-за проблем с точностью с плавающей запятой, которые чаще возникают с необработанными правдоподобиями.Обычно встречающиеся псевдоR-квадраты
ПсевдоR-квадраты Формула Описание Эфрон Зеркала Эфрона приближаются к 1 и 3 из списка выше – остатки модели возводятся в квадрат, суммируются и делятся на общее изменчивость зависимой переменной, и этот R-квадрат также равен к квадрату корреляции между прогнозируемыми значениями и фактическими ценности.
При рассмотрении Эфрона помните, что остатки модели от логистической регрессии не сопоставимы с таковыми в OLS. Зависимая переменная в логистике регрессия не является непрерывной и прогнозируемое значение (вероятность) является. В OLS прогнозируемые значения и фактические значения непрерывно и в одном и том же масштабе, поэтому их различия легко интерпретируется.

McFadden’s М полный = Модель с предикторами
M перемычка = Модель без предсказатели
Зеркала McFadden приближаются к 1 и 2 из списка выше. Обрабатывается логарифмическая вероятность модели перехвата. как общую сумму квадратов, а логарифмическая вероятность полной модели равна рассматривается как сумма квадратов ошибок (как в подходе 1). Отношение вероятностей предполагает уровень улучшения над моделью перехвата, предлагаемой полной моделью (как в подходе 2). Вероятность находится между 0 и 1, поэтому журнал вероятности равен меньше или равно нулю. Если модель имеет очень низкую вероятность, тогда логарифм вероятности будет иметь большую величину, чем логарифм более вероятной модели. Таким образом, небольшое отношение логарифмических вероятностей указывает на то, что полная модель гораздо лучше подходит, чем пересечение модель. 
Если сравнивать две модели на одних и тех же данных, McFadden’s быть выше для модели с большей вероятностью.
McFadden’s (скорректированный) Скорректированное значение Макфаддена отражает скорректированное значение R-квадрата в OLS на наложение штрафа на модель за включение слишком большого количества предикторов. Если предикторы в модели эффективны, то штраф будет быть небольшой по сравнению с добавленной информацией предикторов. Однако, если модель содержит предикторы, которые не дают достаточного прибавления к модели, то штраф становится заметным и скорректированное R-квадрат может уменьшить с добавлением предиктора, даже если R-квадрат немного увеличивается. Обратите внимание, что возможен отрицательный скорректированный R-квадрат Макфаддена. Кокс и Снелл Зеркала Cox & Snell подходят ко 2 из списка выше.  отношение вероятностей отражает улучшение полной модели по сравнению с
модель перехвата (чем меньше отношение, тем больше
улучшение). Рассмотрим определение Л(М). L(M) – условное
вероятность зависимой переменной с учетом независимых переменных.
Если в наборе данных N наблюдений, то L(M) — это
произведение N таких вероятностей. Таким образом, взяв n th корень произведения L(M) обеспечивает оценку вероятности каждого значения Y.
Cox & Snell’s представляет R-квадрат как преобразование – 2ln[L(M Intercept )/L(M Full )] статистика, используемая для определения сходимости логистической
регрессия. Обратите внимание, что псевдо-R-квадрат Кокса и Снелла имеет максимальное значение, равное
не 1: если полная модель точно предсказывает результат и имеет
вероятность 1, Кокса и Снелла тогда 1- Л(М Перехват ) 2/Н , , что меньше единицы.
отношение вероятностей отражает улучшение полной модели по сравнению с
модель перехвата (чем меньше отношение, тем больше
улучшение). Рассмотрим определение Л(М). L(M) – условное
вероятность зависимой переменной с учетом независимых переменных.
Если в наборе данных N наблюдений, то L(M) — это
произведение N таких вероятностей. Таким образом, взяв n th корень произведения L(M) обеспечивает оценку вероятности каждого значения Y.
Cox & Snell’s представляет R-квадрат как преобразование – 2ln[L(M Intercept )/L(M Full )] статистика, используемая для определения сходимости логистической
регрессия. Обратите внимание, что псевдо-R-квадрат Кокса и Снелла имеет максимальное значение, равное
не 1: если полная модель точно предсказывает результат и имеет
вероятность 1, Кокса и Снелла тогда 1- Л(М Перехват ) 2/Н , , что меньше единицы.Нагелькерке / Cragg & Uhler’s Зеркала Nagelkerke/Cragg & Uhler подходят ко 2 из списка выше.  Он настраивает Кокса и Снелла так, чтобы диапазон возможных значений расширялся до
1.Для этого R-квадрат Кокса и Снелла делится на его максимальное значение.
возможное значение, 1- L(M Intercept ) 2/N . Затем, если полная модель точно предсказывает результат и имеет
вероятность 1, R-квадрат Нагелькерке/Крэгга и Улера = 1. Когда L (M полных ) = 1 , тогда R 2 = 1 ;
Когда L(M полное ) = L(M пересечение ) , тогда Ч 2 = 0 .
Он настраивает Кокса и Снелла так, чтобы диапазон возможных значений расширялся до
1.Для этого R-квадрат Кокса и Снелла делится на его максимальное значение.
возможное значение, 1- L(M Intercept ) 2/N . Затем, если полная модель точно предсказывает результат и имеет
вероятность 1, R-квадрат Нагелькерке/Крэгга и Улера = 1. Когда L (M полных ) = 1 , тогда R 2 = 1 ;
Когда L(M полное ) = L(M пересечение ) , тогда Ч 2 = 0 .МакКелви и Завойна
Зеркала McKelvey & Zavoina приближаются к 1 из списка выше, но его расчеты основаны на прогнозировании непрерывной скрытой переменной, лежащей в основе наблюдаемые результаты 0-1 в данных. Прогнозы модели скрытая переменная может быть рассчитана с использованием коэффициентов модели (НЕ логарифмических шансов) и переменные-предикторы.  Маккелви и Завойна также отражают
подход 3. Из-за параллельной структуры между
McKelvey & Zavoina и OLS R-квадраты, мы можем исследовать квадратный корень
McKelvey & Zavoina, чтобы прийти к корреляции между латентным
непрерывная переменная и предсказанные вероятности. Обратите внимание, что, поскольку y* не наблюдается, мы не можем вычислить
дисперсия ошибки (второй член в знаменателе). это
предполагается равным π 2 /3 в логистике
модели.
Маккелви и Завойна также отражают
подход 3. Из-за параллельной структуры между
McKelvey & Zavoina и OLS R-квадраты, мы можем исследовать квадратный корень
McKelvey & Zavoina, чтобы прийти к корреляции между латентным
непрерывная переменная и предсказанные вероятности. Обратите внимание, что, поскольку y* не наблюдается, мы не можем вычислить
дисперсия ошибки (второй член в знаменателе). это
предполагается равным π 2 /3 в логистике
модели.Кол-во Count R-Squared никоим образом не приближается к точности соответствия сравнимо с любым подходом OLS. Он превращает непрерывное предсказанные вероятности в двоичную переменную того же масштаба, что и переменная результата (0-1), а затем оценивает прогнозы как правильные или неправильно. Count R-Square обрабатывает любую запись с прогнозируемой вероятностью 0,5 или выше, как имеющий прогнозируемый результат 1 и любую запись с прогнозируемая вероятность меньше 0,5 как прогнозируемый результат 0.  Затем предсказанные единицы, которые соответствуют фактическим единицам и предсказанным
0, совпадающие с фактическими 0, подсчитываются. Это количество
записи правильно предсказаны, учитывая эту точку отсечки 0,5. R-квадрат
это правильный счет, разделенный на общий счет.
Затем предсказанные единицы, которые соответствуют фактическим единицам и предсказанным
0, совпадающие с фактическими 0, подсчитываются. Это количество
записи правильно предсказаны, учитывая эту точку отсечки 0,5. R-квадрат
это правильный счет, разделенный на общий счет.Скорректированный счет n = количество наиболее частых исходов
Скорректированное количество зеркал R-Square приближается к 2 из приведенного выше списка. Эта корректировка не связана с количеством предикторов и не сравнимо с поправкой на OLS или R-квадраты Макфаддена. такой сценарий: если вас попросят предсказать, кто в списке из 100 случайных человек левша или правша, можно догадаться, что каждый в списке правша, и вы были бы правы для большинства список. Ваше предположение можно рассматривать как нулевую модель. Скорректированное число R-Squared управляет такой нулевой моделью. Ничего не зная о предсказателях, всегда можно было предсказать большее общий результат и быть правым в большинстве случаев.  Эффективная модель
должна улучшить эту нулевую модель, и поэтому эта нулевая модель является базовой линией, для которой Count R-Square
регулируется. Скорректированный счетчик R-квадрат затем измеряет
доля правильных прогнозов за пределами этого базового уровня.
Эффективная модель
должна улучшить эту нулевую модель, и поэтому эта нулевая модель является базовой линией, для которой Count R-Square
регулируется. Скорректированный счетчик R-квадрат затем измеряет
доля правильных прогнозов за пределами этого базового уровня.Краткий пример
Логистическая регрессия была проведена для 200 наблюдений в Stata. Подробнее о данных и модели см. Аннотированный вывод для логистической регрессии в Stata. После запуска модели ввод команды fitstat дает несколько показателей согласия. Вы можете скачать fitstat из Stata, набрав search spost9_ado (см. Как я могу использовать команду поиска искать программы и получать дополнительную помощь? для получения дополнительной информации о используя поиск ).
использовать https://stats.idre.ucla.edu/stat/stata/notes/hsb2, очистить сгенерировать honcomp = (записать >=60) logit honcomp female read science
fitstat, sav(r2_1) Меры соответствия для логита honcomp Только перехват Log-Lik: -115,644 Полная модель Log-Lik: -80,118 Д(196): 160,236 LR(3): 71,052 Вероятность > LR: 0,000 McFadden's R2: 0,307 McFadden Adj R2: 0,273 ML (Кокс-Снелл) R2: 0,299 Крэгг-Улер(Нагелькерке) В2: 0,436 R2 Маккелви и Завойны: 0,519 R2 Эфрона: 0,330 Дисперсия y*: 6,840 Дисперсия ошибки: 3,290 Счетчик R2: 0,810 Регулируемый счет R2: 0,283 АИК: 0,841 АИК*n: 168,236 БИК: -878,234 БИК': -55,158 BIC, используемый Stata: 181,430 AIC, используемый Stata: 168,236Предоставляет несколько псевдо-R-квадратов (и информацию, необходимую для рассчитать еще несколько).
 Обратите внимание, что псевдоR-квадраты меняются
сильно отличаются друг от друга в рамках одной модели. Из несчетных
статистические данные варьируются от 0,273 (с поправкой Макфаддена) до 0,519 (с поправкой МакКелви).
и Завойна).
Обратите внимание, что псевдоR-квадраты меняются
сильно отличаются друг от друга в рамках одной модели. Из несчетных
статистические данные варьируются от 0,273 (с поправкой Макфаддена) до 0,519 (с поправкой МакКелви).
и Завойна).Интерпретация R-квадрата МНК относительно проста: доля общей изменчивости результата, которая приходится на модель». При построении модели цель обычно состоит в том, чтобы предсказать изменчивость. Переменная результата имеет диапазон значений, и вам интересно знать какие обстоятельства каким частям ареала соответствуют. Если вы ищете стоимость жилья, просмотр списка цен на жилье даст вы чувствуете диапазон цен на жилье. Вы можете построить модель, которая включает переменные, такие как местоположение и квадратные футы, чтобы объяснить диапазон цен. Если значение R-квадрата такой модели равно 0,72, то переменные в вашей Модель предсказала 72% изменчивости цен. Таким образом, большинство изменчивость учтена, но если вы хотите улучшить свою модель, вы можете рассмотреть возможность добавления переменных.
 Аналогичным образом можно построить модель
который прогнозирует результаты тестов для учащихся в классе, используя часы обучения и
предыдущая тестовая оценка в качестве предикторов. Если ваше значение R-квадрата из этой модели
равно 0,75, то ваша модель предсказала 75% изменчивости оценок.
Хотя вы предсказали две разные переменные результата в двух разных
наборы данных с использованием двух разных наборов предикторов, вы можете сравнить эти модели
используя их значения R-квадрата: две модели смогли предсказать аналогичные
пропорции изменчивости в их соответствующих результатах, но результаты теста
Модель предсказала несколько более высокую долю изменчивости исхода, чем
Модель цен на жилье. Такое сравнение невозможно с использованием псевдо-R-квадратов.
Аналогичным образом можно построить модель
который прогнозирует результаты тестов для учащихся в классе, используя часы обучения и
предыдущая тестовая оценка в качестве предикторов. Если ваше значение R-квадрата из этой модели
равно 0,75, то ваша модель предсказала 75% изменчивости оценок.
Хотя вы предсказали две разные переменные результата в двух разных
наборы данных с использованием двух разных наборов предикторов, вы можете сравнить эти модели
используя их значения R-квадрата: две модели смогли предсказать аналогичные
пропорции изменчивости в их соответствующих результатах, но результаты теста
Модель предсказала несколько более высокую долю изменчивости исхода, чем
Модель цен на жилье. Такое сравнение невозможно с использованием псевдо-R-квадратов.Какие характеристики псевдоR-квадратов позволяют проводить широкие сравнения псевдоR-квадратов инвалид?
Шкала – OLS R-квадрат находится в диапазоне от 0 до 1, что имеет смысл как для потому что это пропорция и потому что это квадрат корреляции.
 Самый
псевдоR-квадраты не находятся в диапазоне от 0 до 1. Для примера псевдо R-квадрата
который не находится в диапазоне от 0 до 1, рассмотрим псевдо-R-квадрат Кокса и Снелла. В качестве
указано в таблице выше, если полная модель точно предсказывает результат
и имеет вероятность 1, тогда псевдо-R-квадрат Кокса и Снелла равен 1- Л(М Перехват ) 2/Н , , что меньше единицы. Если две логистические модели, каждая с N наблюдения, предсказывают различные результаты, и оба предсказывают их соответствующие
идеально, то псевдо-R-квадрат Кокса и Снелла для двух моделей равен
(1- Л(М Перехват ) 2/Н ). Однако это значение не
то же самое для двух моделей. Модели предсказывали свои результаты одинаково
ну а этот псевдо R-квадрат у одной модели будет выше, чем у другой,
предлагает лучшую посадку. Таким образом, эти псевдоR-квадраты нельзя сравнивать
этим способом.
Самый
псевдоR-квадраты не находятся в диапазоне от 0 до 1. Для примера псевдо R-квадрата
который не находится в диапазоне от 0 до 1, рассмотрим псевдо-R-квадрат Кокса и Снелла. В качестве
указано в таблице выше, если полная модель точно предсказывает результат
и имеет вероятность 1, тогда псевдо-R-квадрат Кокса и Снелла равен 1- Л(М Перехват ) 2/Н , , что меньше единицы. Если две логистические модели, каждая с N наблюдения, предсказывают различные результаты, и оба предсказывают их соответствующие
идеально, то псевдо-R-квадрат Кокса и Снелла для двух моделей равен
(1- Л(М Перехват ) 2/Н ). Однако это значение не
то же самое для двух моделей. Модели предсказывали свои результаты одинаково
ну а этот псевдо R-квадрат у одной модели будет выше, чем у другой,
предлагает лучшую посадку. Таким образом, эти псевдоR-квадраты нельзя сравнивать
этим способом.Некоторые псевдоR-квадраты находятся в диапазоне от 0 до 1, но только поверхностно и более близко соответствуют масштабу МНК R-квадрат.
 Например,
Nagelkerke/Cragg & Uhler’s
псевдо-R-квадрат — это скорректированный коэффициент Кокса и Снелла, который масштабируется с коэффициентом 1/(
1- Л(М Перехват ) 2/Н ).
Это также создает проблемы при сравнении моделей. Рассмотрим два
логистические модели, каждая из которых содержит N наблюдений,
прогнозирование различных результатов и
неспособность улучшить модель перехвата. то есть L(M Полный )/L(M Пересечение )= 1
для обеих моделей. Возможно, эти модели предсказали их соответствующие
результаты одинаково плохи. Тем не менее, две модели будут иметь разные
Nagelkerke/Cragg & Uhler’s
псевдо R-квадраты. Таким образом, эти псевдоR-квадраты нельзя сравнивать в
Сюда.
Например,
Nagelkerke/Cragg & Uhler’s
псевдо-R-квадрат — это скорректированный коэффициент Кокса и Снелла, который масштабируется с коэффициентом 1/(
1- Л(М Перехват ) 2/Н ).
Это также создает проблемы при сравнении моделей. Рассмотрим два
логистические модели, каждая из которых содержит N наблюдений,
прогнозирование различных результатов и
неспособность улучшить модель перехвата. то есть L(M Полный )/L(M Пересечение )= 1
для обеих моделей. Возможно, эти модели предсказали их соответствующие
результаты одинаково плохи. Тем не менее, две модели будут иметь разные
Nagelkerke/Cragg & Uhler’s
псевдо R-квадраты. Таким образом, эти псевдоR-квадраты нельзя сравнивать в
Сюда.Намерение – Отзыв что OLS минимизирует квадраты различий между прогнозами и фактические значения прогнозируемой переменной. Это не относится к логистике. регресс. Способ расчета R-квадрата в регрессии МНК фиксирует, насколько хорошо модель делает то, к чему стремится.
 Различные методы
псевдо-R-квадрата отражают различные интерпретации целей
модель. При оценке модели следует помнить об этом. За
Например, R-квадрат Эфрона и R-квадрат графа оценивают модели в соответствии с
очень разные критерии: оба изучают остатки — разница
между значениями результатов и прогнозируемыми вероятностями, но они рассматривают
остатки очень разные. Эфрон суммирует квадраты остатков и оценивает
модель, основанная на этой сумме. Два наблюдения с небольшими различиями в
их остатки (скажем, 0,49против 0,51) будут иметь небольшие различия в их
квадраты остатков, и эти предсказания Эфрона считают похожими.
С другой стороны, подсчет R-квадрата оценивает модель исключительно на основе того, что
доля остатков меньше 0,5. Таким образом, два наблюдения
с остатками 0,49 и 0,51 рассматриваются совершенно по-разному: наблюдение
с невязкой 0,49 считается «правильным» прогнозом, в то время как
наблюдение с невязкой 0,51 считается «неверным» прогнозом.
При сравнении двух логистических моделей, предсказывающих разные результаты, намерение
моделей не могут быть захвачены одним псевдо R-квадратом, и сравнение
модели с одним псевдо-R-квадратом могут быть обманчивы.
Различные методы
псевдо-R-квадрата отражают различные интерпретации целей
модель. При оценке модели следует помнить об этом. За
Например, R-квадрат Эфрона и R-квадрат графа оценивают модели в соответствии с
очень разные критерии: оба изучают остатки — разница
между значениями результатов и прогнозируемыми вероятностями, но они рассматривают
остатки очень разные. Эфрон суммирует квадраты остатков и оценивает
модель, основанная на этой сумме. Два наблюдения с небольшими различиями в
их остатки (скажем, 0,49против 0,51) будут иметь небольшие различия в их
квадраты остатков, и эти предсказания Эфрона считают похожими.
С другой стороны, подсчет R-квадрата оценивает модель исключительно на основе того, что
доля остатков меньше 0,5. Таким образом, два наблюдения
с остатками 0,49 и 0,51 рассматриваются совершенно по-разному: наблюдение
с невязкой 0,49 считается «правильным» прогнозом, в то время как
наблюдение с невязкой 0,51 считается «неверным» прогнозом.
При сравнении двух логистических моделей, предсказывающих разные результаты, намерение
моделей не могут быть захвачены одним псевдо R-квадратом, и сравнение
модели с одним псевдо-R-квадратом могут быть обманчивы.
Для некоторого контекста мы можем изучить другую модель, предсказывающую ту же переменную в том же наборе данных, что и модель выше, но с одной добавленной переменной. Stata позволяет нам сравнить статистику соответствия этой новой модели и предыдущей. модель бок о бок.
logit honcomp female read science math
fitstat, using(r2_1) Меры соответствия для логита honcomp Текущая сохраненная разница Модель: логит логит Н: 200 200 0 Только перехват Log-Lik -115,644 -115,644 0,000 Полная модель Log-Lik -73,643 -80,118 6,475 Д 147.286(195) 160,236(196) 12,951(1) ЛР 84.003(4) 71.052(3) 12.951(1) Вероятность > LR 0,000 0,000 0,000 R2 Макфаддена 0,363 0,307 0,056 Корректировка Макфаддена R2 0,320 0,273 0,047 ML (Кокса-Снелла) R2 0,343 0,299 0,044 Крэгг-Улер (Нагелькерке) R2 0,500 0,436 0,064 МакКелви и Завойна R2 0,560 0,5190,041 R2 Эфрона 0,388 0,330 0,058 Дисперсия у* 7,485 6,840 0,645 Дисперсия ошибки 3,290 3,290 0,000 Подсчет R2 0,840 0,810 0,030 Adj Count R2 0,396 0,283 0,113 АИК 0,786 0,841 -0,055 АИК*n 157,286 168,236 -10,951 БИК -885,886 -878,234 -7,652 БИК' -62,810 -55,158 -7,652 БИК, используемый Stata 173,777 181,430 -7,652 AIC, используемый Stata 157,286 168,236 -10,951Все приведенные здесь псевдо-R-квадраты согласны с тем, что эта модель лучше подходит данные о результатах, чем предыдущая модель.
 В то время как псевдо-R-квадраты не могут быть
интерпретируются независимо или сравниваются между наборами данных, они действительны и полезны
при оценке нескольких моделей, предсказывающих один и тот же результат на одном и том же наборе данных.
Другими словами, статистика псевдо-R-квадрата без контекста не имеет большого значения.
Псевдо-R-квадрат имеет смысл только по сравнению с другим псевдо-R-квадратом
того же типа, на тех же данных, предсказывая тот же результат. В этом
ситуации, более высокий псевдо-R-квадрат указывает, какая модель лучше предсказывает
исход.
В то время как псевдо-R-квадраты не могут быть
интерпретируются независимо или сравниваются между наборами данных, они действительны и полезны
при оценке нескольких моделей, предсказывающих один и тот же результат на одном и том же наборе данных.
Другими словами, статистика псевдо-R-квадрата без контекста не имеет большого значения.
Псевдо-R-квадрат имеет смысл только по сравнению с другим псевдо-R-квадратом
того же типа, на тех же данных, предсказывая тот же результат. В этом
ситуации, более высокий псевдо-R-квадрат указывает, какая модель лучше предсказывает
исход.Были предприняты попытки оценить точность различных псевдоR-квадратов с помощью прогнозирование непрерывной скрытой переменной с помощью регрессии МНК и ее наблюдаемых бинарная переменная с помощью логистической регрессии и сравнения псевдо R-квадратов к OLS R-квадрат. В таких симуляциях Маккелви Ближе всего к R-квадрату OLS оказался вариант Завойной.
Ссылки
Фриз, Джереми и Дж. Скотт Лонг. Регрессионные модели для категориальных Зависимые переменные с использованием Stata.


 ..
.. 20 л(85 л.с.),
бензин
хэтчбек, серебряный
автомат, Comfort 1.2 AT
20 л(85 л.с.),
бензин
хэтчбек, серебряный
автомат, Comfort 1.2 AT 20 л(85 л.с.),
бензин
хэтчбек, красный
автомат, Comfort 1.2 AT
20 л(85 л.с.),
бензин
хэтчбек, красный
автомат, Comfort 1.2 AT

 9 литров на 100 км.
9 литров на 100 км. Отсюда разделите первую сумму ошибок (объясненная дисперсия) на вторую сумму (общая дисперсия), вычтите результат из единицы, и вы получите R-квадрат.
Отсюда разделите первую сумму ошибок (объясненная дисперсия) на вторую сумму (общая дисперсия), вычтите результат из единицы, и вы получите R-квадрат.
 Таким образом, может показаться, что модель с большим количеством членов лучше подходит только потому, что в ней больше членов, в то время как скорректированный R-квадрат компенсирует добавление переменных и увеличивается только в том случае, если новый член улучшает модель по сравнению с тем, что было бы. получается по вероятности и уменьшается, когда предиктор улучшает модель меньше, чем предсказано случайно.
Таким образом, может показаться, что модель с большим количеством членов лучше подходит только потому, что в ней больше членов, в то время как скорректированный R-квадрат компенсирует добавление переменных и увеличивается только в том случае, если новый член улучшает модель по сравнению с тем, что было бы. получается по вероятности и уменьшается, когда предиктор улучшает модель меньше, чем предсказано случайно.

 Предположим, вы ищете индексный фонд, который будет максимально точно отслеживать конкретный индекс. В этом сценарии вы хотели бы, чтобы R-Squared фонда был как можно выше, поскольку его цель — соответствовать индексу, а не превышать его. С другой стороны, если вы ищете активно управляемые фонды, высокий R-квадрат может рассматриваться как плохой знак, указывающий на то, что управляющие фондами не добавляют достаточной ценности по сравнению с их контрольными показателями.
Предположим, вы ищете индексный фонд, который будет максимально точно отслеживать конкретный индекс. В этом сценарии вы хотели бы, чтобы R-Squared фонда был как можно выше, поскольку его цель — соответствовать индексу, а не превышать его. С другой стороны, если вы ищете активно управляемые фонды, высокий R-квадрат может рассматриваться как плохой знак, указывающий на то, что управляющие фондами не добавляют достаточной ценности по сравнению с их контрольными показателями. В этом посте мы рассмотрим R-квадрат (R 2 ), выделите некоторые его ограничения и обнаружите несколько сюрпризов. Например, малые значения R-квадрата не всегда являются проблемой, а высокие значения R-квадрата не обязательно хороши!
В этом посте мы рассмотрим R-квадрат (R 2 ), выделите некоторые его ограничения и обнаружите несколько сюрпризов. Например, малые значения R-квадрата не всегда являются проблемой, а высокие значения R-квадрата не обязательно хороши! Беспристрастность в этом контексте означает, что подобранные значения не являются систематически слишком высокими или слишком низкими где-либо в пространстве наблюдения.
Беспристрастность в этом контексте означает, что подобранные значения не являются систематически слишком высокими или слишком низкими где-либо в пространстве наблюдения.



 График «Остатки против подгонки» подчеркивает эту нежелательную закономерность. Несмещенная модель имеет остатки, которые случайным образом разбросаны вокруг нуля. Неслучайные остаточные паттерны указывают на плохое соответствие, несмотря на высокое значение R 2 . Всегда проверяйте остаточные участки!
График «Остатки против подгонки» подчеркивает эту нежелательную закономерность. Несмещенная модель имеет остатки, которые случайным образом разбросаны вокруг нуля. Неслучайные остаточные паттерны указывают на плохое соответствие, несмотря на высокое значение R 2 . Всегда проверяйте остаточные участки!

 Если наша мера будет работать хорошо, она должна уметь различать эти две совершенно разные ситуации.
Если наша мера будет работать хорошо, она должна уметь различать эти две совершенно разные ситуации.
 Наклон оценочной линии регрессии намного круче, что позволяет предположить, что по мере увеличения предиктора x происходит довольно существенное изменение (уменьшение) отклика 92=8487,8\)
Наклон оценочной линии регрессии намного круче, что позволяет предположить, что по мере увеличения предиктора x происходит довольно существенное изменение (уменьшение) отклика 92=8487,8\) 0218 r 2 можно интерпретировать. Мы говорим либо:
0218 r 2 можно интерпретировать. Мы говорим либо: Вариант второй интерпретации состоит в том, чтобы сказать: « r 2 × 100 процентов вариации в y объясняется изменением предиктора x ».
Вариант второй интерпретации состоит в том, чтобы сказать: « r 2 × 100 процентов вариации в y объясняется изменением предиктора x ».



 Метод минимизирует сумму квадратов остатков. С помощью графиков остатков можно проверить, согласуется ли наблюдаемая ошибка со стохастической ошибкой (различия между ожидаемыми и наблюдаемыми значениями должны быть случайными и непредсказуемыми).
Метод минимизирует сумму квадратов остатков. С помощью графиков остатков можно проверить, согласуется ли наблюдаемая ошибка со стохастической ошибкой (различия между ожидаемыми и наблюдаемыми значениями должны быть случайными и непредсказуемыми).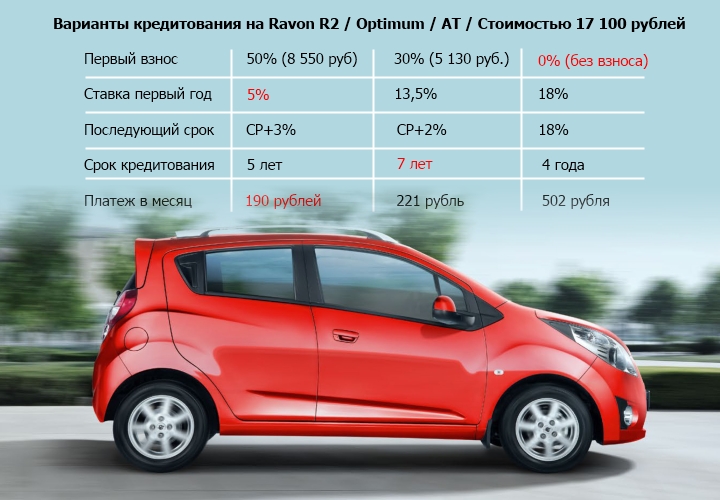

 Среднее значение зависимой переменной помогает предсказать зависимую переменную, а также модель регрессии.
Среднее значение зависимой переменной помогает предсказать зависимую переменную, а также модель регрессии. Он иллюстрирует, как значения R-квадрата представляют разброс вокруг линии регрессии.
Он иллюстрирует, как значения R-квадрата представляют разброс вокруг линии регрессии. Обычно, когда значение R 2 высокое, это предполагает лучшее соответствие модели.
Обычно, когда значение R 2 высокое, это предполагает лучшее соответствие модели.
