Объём цилиндра. Калькулятор объёма цилиндра онлайн
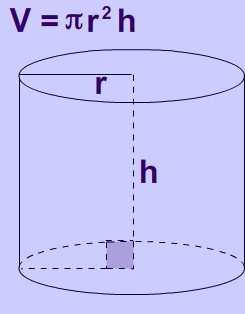
Объем цилиндра равен произведению квадрата радиуса основания, высоты цилиндра и числа пи (3.1415)
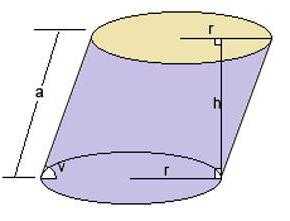
Цилиндр – это геометрическое тело, которое имеет цилиндрическую поверхность, называемое еще как боковая поверхность цилиндра и имеет две поверхности, которые носят название оснований цилиндра. Круговым цилиндр называют, если у него в основании лежит круг.
Высота цилиндра — это отрезок, соединяющий две любые точки оснований но обязательно расположенный перпендикулярно к ним обоим.
Объем прямого цилиндра
Цилиндр — это геометрическое тело, которое сформировано вращением прямоугольника на оси, совпадающей с одним из его сторон. Слово «цилиндр» происходит от греческого слова «kylindros».
Объем цилиндра через радиус основания и высоту цилиндра
Объем цилиндра равен произведению квадрата радиуса основания, высоты цилиндра и числа пи (3.1415)
\[ \LARGE V = \pi \cdot R^{2} \cdot H \]
где:
V — объем цилиндра
π — число пи (3.1415)
R — радиус основания
H — высота цилиндра
Объем цилиндра через площадь основания и высоту цилиндра
Объем цилиндра равен произведению площади основания цилиндра на его высоту.
\[ \LARGE V = S \cdot H \]
где:
V — объем цилиндра
H — высота цилиндра
S — площадь цилиндра
Объем цилиндра через диаметр основания и высоту цилиндра
Объем цилиндра равен произведению диаметра основания и числа пи (3.1415) делённое на четыре высоты цилиндра
\[ \LARGE V = \frac {\pi \cdot D^{2} }{4 \cdot H} \]
где:
V — объем цилиндра
π — число пи (3.1415)
D — диаметр основания
H — высота цилиндра
Калькулятор объёма цилиндра
Входные данные
Радиус цилиндра r:
Высота цилиндра h:
Количество знаков после запятой в результате вычислений
1234567
Результат
В вашем браузере отключен Javascript.Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!
Не можешь написать работу сам?
Доверь её нашим специалистам
от 100 р.стоимость заказа
2 часамин. срок
Узнать стоимость
Поделитесь с другими:
Если материал понравился Вам и оказался для Вас полезным, поделитесь им со своими друзьями!
calcsbox.com
Цилиндр. Формулы и свойства
Определение.
Цилиндр — это геометрическое тело, ограниченное цилиндрической поверхностью и двумя плоскостями (основами цилиндраЦилиндрическая поверхность — поверхность, получаемая при движении прямой (образующей L) параллельно самой себе, вдоль плоской кривой направляющей.
Основания цилиндра — плоские фигуры, образованные пересечением цилиндрической поверхности с двумя плоскостями.
Круговой цилиндр
В большинстве случаев под цилиндром подразумевается прямой круговой цилиндр, у которого направляющая — окружность, а основания перпендикулярны образующей. У такого цилиндра имеется ось симметрии.
Прямой круговой цилиндр можно описать, как объёмного фигуру, образующуюся вращением прямоугольника вокруг своей стороны на 360°.
Определение. Радиус цилиндра r — это радиус основания цилиндра.
Определение. Диаметр цилиндра d — это диаметр основания цилиндра.
Определение. Высота цилиндра h — это расстояние между основаниями цилиндра.
Определение. Ось цилиндра — это прямая O 1O2, которая проходит через центры оснований цилиндра.
Определение. Поверхность цилиндра состоит из цилиндрической поверхности и оснований цилиндра.
Определение. Осевое сечение цилиндра — это сечение цилиндра плоскостью, проходящей через ось цилиндра.
Определение. Касательная плоскость к цилиндру — это плоскость, которая проходит через образующую цилиндра и перпендикулярно к осевому сечении цилиндра.
Формула. Объём цилиндра:| V = πr2h = π | d2 | h , |
| 4 |
Sb = 2πrh = πdh
Формула. Полная площадь поверхности цилиндра:S = 2πr(h + r)
Косой цилиндр — цилиндр, основы которого не параллельны (Рис.2)
Наклонный цилиндр — цилиндр, у которого образующие не перпендикулярно основам цилиндра (Рис.3 — наклонный круговой цилиндр).
ru.onlinemschool.com
Объем цилиндра: формула, калькулятор — 24СМИ
Как отличить человека технической специальности от человека с гуманитарным складом ума? Спросите каждого, что такое цилиндр. Первый скажет, что это геометрическое тело, второй вспомнит мужской головной убор 19 века. Оба будут правы, да и шляпа получила такое название благодаря особенной форме, основой которой являлась та самая фигура из геометрии. Итак, каковы особенности цилиндра и как рассчитать его объем.
Расчет объема цилиндра
Слово «цилиндр» произошло от древнегреческого kylindros, означающего «валик». Математики дают несколько определений цилиндру:
- Цилиндр — геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими ее под прямым углом.
- Цилиндр — это тело вращения, которое получается при вращении прямоугольника вокруг его стороны.
- Цилиндр — геометрическое тело, которое сформировано вращением прямоугольника на оси, совпадающей с одной из его сторон.
Фигура цилиндрВсе эти определения верны. Также стоит отметить основные части цилиндра:
- Основания — плоские фигуры, образованные пересечением цилиндрической поверхности с двумя параллельными плоскостями.
- Боковая поверхность цилиндра — поверхность между плоскостями оснований.
Если в основании цилиндра лежит круг, то его называют круговым. Существуют и другие виды цилиндров, в зависимости от формы основания — эллиптический, гиперболический, параболический и т.д.
Также все цилиндры делятся на прямые и наклонные. У каждого цилиндра есть образующие — это отрезки, соединяющие соответствующие точки оснований. Если образующие перпендикулярны основаниям, то цилиндр называется прямым, а если образующие расположены под углом — цилиндр наклонный или косой.
Рисунок цилиндраЕсть и другие общие понятия для цилиндров:
- Основания цилиндра равны и лежат в параллельных плоскостях. У цилиндра образующие параллельны и равны.
- Поверхность цилиндра состоит из оснований и боковой поверхности. Боковая поверхность составлена из образующих.
- Радиусом цилиндра называется радиус его основания.
- Высотой цилиндра называется расстояние между плоскостями оснований.
- Осью цилиндра называется прямая, проходящая через центры оснований.
- Сечение цилиндра плоскостью, проходящей через ось цилиндра, называется осевым сечением.
- Плоскость, проходящая через образующую прямого цилиндра и перпендикулярная осевому сечению, проведенному через эту образующую, называется касательной плоскостью цилиндра.
Итак, как же вычислить объем цилиндра. Посчитать объем прямого кругового цилиндра можно на калькуляторе. Он равен произведению площади основания на высоту.
V = πR2h,
где V — объем цилиндра, R — радиус основания, h — высота цилиндра, а «пи» — константа, равная 3,14.
Объем цилиндрТаким же образом вычисляется объем прямого кругового цилиндра через диаметр окружности основания — d.
V = πhd2/4
Если цилиндр прямой, но не круговой, то формула вычисления объема представляет произведение длины образующей – n на площадь сечения цилиндра плоскостью, перпендикулярной образующей — S.
V = n * S
Наклонный цилиндрЕсли цилиндр наклонный, то в формуле участвует и синус угла наклона (альфа) образующей к основанию. В этом случае объем вычисляется по формуле:
V = S * n * sin α
Исчисляется объем цилиндра в кубических единицах.
Если стоит задача найти объем описанного вокруг сферы цилиндра, то расчеты будут такими:
Цилиндр и сфераРадиус цилиндра равен радиусу сферы — R. Высота цилиндра равна диаметру сферы. Диаметр есть удвоенный радиус — 2R. Таким образом объем прямого описанного цилиндра равен произведению площади основания πR2 («пи» умножить на радиус в квадрате) на высоту, т. е. 2R.
V = 2R * πR2
Приведя формулу к должному виду получим:
V = 2πR3
Если цилиндр вписан в прямоугольный параллелепипед, то, зная длину стороны его основания и высоту, можно найти объем.
Цилиндр, вписанный в параллелепипедВ этом случае радиус основания цилиндра равен половине длины стороны основания параллелепипеда — а. Высота цилиндра и параллелепипеда совпадают, обозначим h. Тогда объем вычисляется по формуле:
V = πh(a/2)2
Где применяется расчет объема цилиндра
Расчет объема цилиндра учащиеся проходят в средней школе. Во взрослой жизни эти знания применяют в своей работе инженеры и конструкторы различных машин и механизмов, потребительских товаров, а также архитекторы.
Из товаров народного потребления форму цилиндра имеют стаканы, кружки, бокалы, кастрюли, термосы и прочая посуда, а также некоторые вазы, банки и упаковки напитков либо средств бытовой химии. Объем таких цилиндрических предметов исчисляется в литрах.
Стаканы имеют цилиндрическую формуРассчитывается объем цилиндра при производстве медицинских шприцов. От полученного объема зависит точное количество медикаментов, вводимое пациенту при инъекциях. Лекарства в жидкой форме, суспензии, растворы помещаются в стеклянные или пластиковые бутылочки цилиндрической формы, а на бирке указывается объем средства.
Распространены цилиндры и в технике: такой вид имеют валы и их отдельные составные части, используемые в двигателях внутреннего сгорания. К тому же, расчет объема цилиндра – задача, которую приходится решать конструкторам при проектировании современных бензиновых и дизельных силовых агрегатов, ведь от этого параметра зависят характеристики, в первую очередь, мощность. Двигатели внутреннего сгорания снабжаются поршнями, которые также имеют цилиндрическую форму.
Расчет цилиндрического валаАрхитекторам приходится рассчитывать объем цилиндра при проектировании зданий, снабженных колоннами. Правда, эти архитектурные элементы в классическом варианте (вместе с базой и капителем) встречаются редко, но упрощенные разновидности, состоящие из одного ствола (который и представляет собой цилиндр) используются часто.
Чрезвычайно распространенные детали, которые присутствуют в конструкциях технических устройств — роликовые подшипники. Как нетрудно догадаться по названию, главный компонент — прочные и износостойкие металлические цилиндрические ролики. Благодаря такой геометрии, эти детали обладают большой несущей способностью и способны выдерживать нагрузки. Роликовые подшипники — высокоточные детали, и поэтому при их создании правильный расчет объема цилиндра (ролика) играет немаловажную роль.
24smi.org
формулы и задача :: SYL.ru
Вопрос, как найти объем цилиндра, может возникнуть не только у школьника. Ведь такую форму имеет, к примеру, кастрюля, емкость которой иногда срочно нужно узнать. Вот тогда потребуется знание специальной формулы.
Что нужно знать о цилиндре?
Геометрическое тело, о котором мы говорим, образуется в результате вращения прямоугольника вокруг одной из его сторон, и всегда будет прямым. То есть угол между образующей цилиндра и его основанием в данном случае равен 90 градусам. Если выполнить это простое движение не удается, и угол уже не 90 градусов, то идет речь о наклонном цилиндре.
Каким бы ни был вид тела, все равно нужно знать о том, как найти объем цилиндра. Но сначала нужно определиться с некоторыми теоретическими данными.
Как называются отдельные элементы цилиндра и что о них известно?
Отрезки, которые соединяют попарно соответствующие точки на двух основаниях, называются образующими. У любого цилиндра они равны и параллельны друг другу. Если он прямой, то длина образующей совпадает с высотой тела.
В основании может лежать окружность или эллипс, тогда цилиндр будет круговым или эллиптическим соответственно. В формулах этот факт потребуется учесть. Потому что чаще всего они даются для кругового цилиндра. В эллиптическом, до того как вычислить объем цилиндра, нужно будет узнать, по какой формуле определить площадь овала.
Формулы объема для прямого и наклонного цилиндров
Здесь и далее приняты такие обозначения.
| Буква-обозначение | математическая величина |
| V | объем |
| S | площадь основания |
| h | высота |
| r | радиус окружности |
| l | длина образующей |
| α | угол между образующей и основанием |
В любом случае потребуется формула, в которой высота тела, умножается на площадь основания. Она выглядит так:
V = Sh
Если требуется узнать, как найти объем цилиндра прямого, то здесь высота по длине полностью совпадает с образующей. Основанием чаще всего является круг, тогда его площадь будет сосчитана по формуле:
S = πr2.
Когда в задаче идет речь об эллиптическом цилиндре, то потребуется такая формула площади основания:
S = π ab, здесь буквами a и b обозначены малая и большая полуоси овала.
При решении задач о наклонном цилиндре потребуется ввести некоторые дополнения в формулу. Например, если не известна высота, но идет речь об образующей и угле между ней и основанием. Тогда букву h потребуется заменить таким выражением:
h = l * sin α.
Как быть, если нужно определить объем на практике?
В задачах обычно уже известны значения угла или высоты с образующей. А возможно, какие-то другие элементы, через которые их можно найти. В жизни приходится делать измерения самостоятельно.
Тогда вопрос о том, как определить объем цилиндра, сводится к тому, чтобы правильно сделать измерения его высоты и радиуса. Для этого потребуются: линейка, карандаш и прямоугольный лист бумаги.
Чаще всего в быту нас окружают прямые круговые цилиндры. Измерить их высоту обычно не составляет труда. Нужно просто приложить линейку сбоку и измерить расстояние от низа до верха тела. Это будет высота — h.
С радиусом окружности все не так легко. Нужно немного вспомнить геометрию. Здесь потребуется лист бумаги с прямым углом и карандаш.
Что дает теория по геометрии? Вокруг прямоугольного треугольника можно описать окружность. Причем его прямой угол окажется на ней, а гипотенуза совпадет с диаметром.
Нужно взять лист бумаги и положить его так, чтобы прямой угол касался края основания. Тогда две его стороны, которые образуют этот угол, в некоторых точках пересекутся с окружностью. В этих местах потребуется сделать метки. По ним провести отрезок. Он окажется гипотенузой и искомым диаметром основания цилиндра.
Как найти объем цилиндра, в нашем случае? В формуле фигурирует радиус. Он равен половине диаметра. То есть длину получившегося отрезка нужно разделить на два.
Осталось только подставить результаты измерений в формулу объема и сосчитать. Причем учесть, что ответ получится в см3. Если объем нужно узнать в кубических метрах, то число нужно будет разделить на миллион. Чтобы получить объем в литрах, делителем окажется тысяча.
Задача
Условие. Даны два цилиндра. Высота первого в два раза больше второго. Радиус второго вдвое больше, чем у первого. Необходимо узнать, во сколько раз объем первого цилиндра больше или мегьше объема второго.
Решение. Сначала потребуется ввести обозначения. Пусть высота и радиус первого тела будут иметь индекс 1, а второго — 2.
Теперь можно записать данные в условии значения в виде выражений:
h1 = 2h2 и r2 = 2r1.
Формулы объемов обоих цилиндров примут такой вид:
v1 = π r12 h1 и v2 = π r22 h2.
В задаче требуется найти:
v1 : v2 = (π r12 h1) : (π r22 h2).
После сокращения πи замены h1 и r2введенными выражениями, получается:
v1 : v2 = (r12 2h2) : (4r12 h2).
То есть v1 : v2 = 1 : 2. Это означает, что объем первого цилиндра в два раза меньше.
Ответ. v1 = v2 : 2.
www.syl.ru
Формула нахождения объема цилиндра онлайн
Цилиндром является геометрическое тело, состоящее из цилиндрической боковой поверхности и двух перпендикулярных ее оси плоскостей (оснований). При вращении прямоугольника вокруг любой из его сторон получается цилиндр. В переводе с греческого цилиндр означает каток, валик. Если в основании цилиндра находится круг — это круговой цилиндр. Объем цилиндра рассчитывается 2-мя способами. В 1-м случае объем равняется произведению пл. основания цилиндра на его высоту. Формула для расчета объема цилиндра:
R — радиус вращения;
h – высота.
Расчет объема цилиндра через радиус и высоту
Во втором случае объем цилиндра рассчитывается как произведение квадрата радиуса цилиндра на его высоту и постоянное число пи по формуле:
В данной формуле:
h – высота цилиндра;
S — площадь основания.
Расчет объема цилиндра через площадь основания
infofaq.ru
Формула рабочего объема двигателя, цилиндра
Формула рабочего объема двигателя — это, по сути, формула рабочего объема цилиндра, умноженная на количество цилиндров двигателя. Но, поскольку она публиковалась в разных вариантах, то это может сбивать с толку. Независимо от используемого варианта формулы результат расчета будет одним и тем же.
Изменение рабочего объема двигателя после растачивания цилиндров или изменения хода поршней.
При растачивании цилиндров двигателя со стенок цилиндров снимается слой металла и штатные поршни заменяются ремонтными поршнями, имеющими больший диаметр. Растачивание цилиндров приводит к увеличению как рабочего объема, так и степени сжатия.
Серийный двигатель, уже использовавшийся в предыдущем примере расчета рабочего объема, с диаметром цилиндров 4,000 дюйма и ходом поршней 3,000 дюйма имеет рабочий объем 226 куб. дюймов. Если расточить цилиндры под диаметр, увеличенный на 0.060 дюйма, то диаметр цилиндров станет равным 4,060 дюйма.
Формула для расчета рабочего объема двигателя остается той же, за исключением того, что вместо 4,000 дюймов в нее подставляем 4,060 дюйма.
Рабочий объем двигателя (в кубических дюймах) = диаметр цилиндра х диаметр цилиндра х ход поршня х 0,7854 х число цилиндров
4.060 дюйма х 4,060 дюйма х 3,000 дюйма х 0,7854 х
х 6 = 233 кубических дюйма = 3818 см3.
Если диаметр цилиндров не изменяется, а ход поршней после замены коленчатого вала увеличится, то при этом возрастет как рабочий объем двигателя, так и степень сжатия цилиндров. Если ход поршней увеличивается на 1/8 дюйма (0,125 дюйма), а диаметр цилиндров остается таким же, как у серийного двигателя, расчет нового рабочего объема двигателя производится следующим образом:
Рабочий объем двигателя (в кубических дюймах) = диаметр цилиндра х диаметр цилиндра х ход поршня х 0,7854 х число цилиндров 4,000 дюйма х 4,000 дюйма х 3,125 дюйма х 0,7854 х х 6 = 236 кубических дюймов = 3867 см3.
Рабочий объем цилиндра формула двигателя
При одновременном увеличении диаметра цилиндров (расточены на 0,060 дюйма) и хода поршней (увеличен на 0,125 дюйма) рабочий объем двигателя в результате этих изменений станет равным.
4.060 дюйма х 4,060 дюйма х 3,125 дюйма х 0,7854 х
х 6 = 243 кубических дюйма = 3982 см3.
sovetprost.ru
Расчет массы цилиндра — однородного и полого
Цилиндр является одной из простых объемных фигур, которую изучают в школьном курсе геометрии (раздел стереометрия). При этом часто возникают задачи на расчет объема и массы цилиндра, а также на определение площади его поверхности. Ответы на отмеченные вопросы даны в этой статье.
Что такое цилиндр?
Перед тем как переходить к ответу на вопрос, чему равна масса цилиндра и его объем, стоит рассмотреть, что представляет собой эта пространственная фигура. Сразу необходимо отметить, что цилиндр — это трехмерный объект. То есть в пространстве можно измерить три его параметра по каждой из осей в декартовой прямоугольной системе координат. В действительности для однозначного определения размеров цилиндра достаточно знать всего два его параметра.
Цилиндр — это объемная фигура, образованная двумя кругами и цилиндрической поверхностью. Чтобы яснее представить этот объект, достаточно взять прямоугольник и начать вращать его вокруг какой-либо его стороны, которая будет осью вращения. В этом случае вращающийся прямоугольник опишет фигуру вращения — цилиндр.
Две круглые поверхности называются основаниями цилиндра, они характеризуются определенным радиусом. Расстояние между основаниями называется высотой. Два основания соединены между собой цилиндрической поверхностью. Линия, проходящая через центры обоих кругов, называется осью цилиндра.
Объем и площадь поверхности
Как можно заметить из вышесказанного, цилиндр определяется двумя параметрами: высотой h и радиусом его основания r. Зная эти параметры, можно рассчитать все другие характеристики рассматриваемого тела. Ниже приводятся основные из них:
- Площадь оснований. Эта величина рассчитывается по формуле: S1 = 2*pi*r2, где pi — число пи, равное 3,14. Цифра 2 в формуле появляется потому, что цилиндр имеет два одинаковых основания.
- Площадь цилиндрической поверхности. Ее можно рассчитать так: S2 = 2*pi*r*h. Понять эту формулу просто: если цилиндрическую поверхность разрезать вертикально от одного основания к другому и развернуть, то получится прямоугольник, высота которого будет равна высоте цилиндра, а ширина будет соответствовать длине окружности основания объемной фигуры. Поскольку площадь полученного прямоугольника — это произведение его сторон, которые равны h и 2*pi*r, то получается представленная выше формула.
- Площадь поверхности цилиндра. Она равна сумме площадей S1 и S2, получаем: S3 = S1 + S2 = 2*pi*r2 + 2*pi*r*h = 2*pi*r*(r+h).
- Объем. Эта величина находится просто, необходимо лишь умножить площадь одного основания на высоту фигуры: V = (S1/2)*h = pi*r2*h.
Определение массы цилиндра
Наконец, стоит перейти непосредственно к теме статьи. Как определить массу цилиндра? Для этого необходимо знать его объем, формула для вычисления которого была представлена выше. И плотность вещества, из которого он состоит. Масса определяется по простой формуле: m = ρ*V, где ρ — плотность материала, образующего рассматриваемый объект.
Понятие плотности характеризует массу вещества, которое находится в единице объема пространства. Например. Известно, что железо имеет большую плотность, чем дерево. Это означает, что в случае одинаковых объемов вещества железа и дерева первое будет иметь намного большую массу, чем второе (приблизительно в 16 раз).
Расчет массы медного цилиндра
Рассмотрим простую задачу. Необходимо найти массу цилиндра, сделанного из меди. Для определенности пусть цилиндр имеет диаметр 20 см и высоту 10 см.
Перед тем как приступать к решению задачи, следует разобраться с исходными данными. Радиус цилиндра равен половине его диаметра, значит r = 20/2 = 10 см, высота же составляет h = 10 см. Поскольку рассматриваемый в задаче цилиндр сделан из меди, то, обращаясь к справочным данным, выписываем значение плотности этого материала: ρ = 8,96 г/см3 (для температуры 20 °C).
Теперь можно приступать к решению задачи. Для начала рассчитаем объем: V =pi*r2*h = 3,14*(10)2*10 = 3140 см3. Тогда масса цилиндра будет равна: m = ρ*V = 8,96 * 3140 = 28134 грамм или приблизительно 28 килограмм.
Следует обратить внимание на размерность единиц во время их использования в соответствующих формулах. Так, в задаче все параметры были представлены в сантиметрах и граммах.
Однородный и полый цилиндры
Из полученного выше результата можно видеть, что медный цилиндр с относительно малыми размерами (10 см) обладает большой массой (28 кг). Это связано не только с тем, что он сделан из тяжелого материала, но и с тем, что он является однородным. Этот факт важно понимать, поскольку приведенную выше формулу для расчета массы можно использовать только в случае, если цилиндр полностью (снаружи и внутри) состоит из одного и того же материала, то есть является однородным.
На практике же часто используют полые цилиндры (например, цилиндрические бочки для воды). То есть они сделаны из тонких листов какого-то материала, а внутри являются пустыми. Для полого цилиндра указанной формулой расчета массы пользоваться нельзя.
Интересно рассчитать, какой массой будет обладать цилиндр из меди, если он является пустым внутри. Для примера пусть он будет сделан из тонкого медного листа толщиной всего d = 2 мм.
Чтобы решить эту задачу, нужно найти объем самой меди, из которой сделан объект. А не объем цилиндра. Поскольку толщина листа мала, по сравнению с размерами цилиндра (d = 2 мм и r = 10 см), тогда объем меди, из которой изготовлен предмет, можно найти, если умножить всю площадь поверхности цилиндра на толщину медного листа, получаем: V = d*S3 = d*2*pi*r*(r+h). Подставляя данные из предыдущей задачи, получим: V = 0,2*2*3,14*10*(10+10) = 251,2 см3. Массу полого цилиндра можно получить, если умножить полученный объем меди, который потребовался для его изготовления, на плотность меди: m = 251,2 * 8,96 = 2251 г или 2,3 кг. То есть рассмотренный полый цилиндр весит в 12 (28,1/2,3) раз меньше, чем однородный.
fb.ru